Bash/シェルスクリプトで学ぶビッグオー
ビッグオーとは?
オーダー記法です。
オーダー記法とは、「計算量の割合」です。
例)Aさんの年齢はx歳、130歳以上生きる人間は存在しない。
x<=130となりますので、ビッグオー記法では、
O(130) となります。
例)
相手に「0 以上 32 未満の整数値」をなにか 1 つ思い浮かべてもらい、それを当てたいです。
相手に何回か「Yes / No で答えられる質問」をすることができます。できるだけ少ない回数で当てるにはどうしたらよいでしょうか?
0ですか?
1ですか?
2ですか?
3ですか?
:
:
この方法であれば最悪32回の探索が必要となります。
O(N)でこれは線形探索とアルゴリズムです。
Nは32を表します。
32の半分の16を基準に、
16以上ですか?
はい なら: 0 以上 16 未満だとわかる
いいえ なら: 16 以上 32 未満だとわかる
はい であれば、
8以上ですか?
と、半分に区切り質問していくと5会の質問で数を当てることができます。
O(log(N)) となり、これは二分探索法(バイナリサーチ)となります。
O(1)
配列の添字を使った探索がこれに該当する
要素が多くなっても決まった処理しか行われない
命令数がデータ数に比例することを意味する。
データ量と関係なく、処理時間が一定。
オーダーで最も速い。
#!/usr/bin/bash
#配列
declare -a array=(1 2 3 4 5);
#
##
# 配列の添字アクセス
# <>exec()
function exec(){
local key=$1;
echo "array[$key]: " $(( array[key] ));
}
##
#
exec 3;
O(N)
線形探索がこれに該当する。
偶数出力はこのパターン。
最悪ケースについて考えるパターン。
データ量に応じて処理時間が比例する
for文で配列の中身をくまなく調べる場合がこれ
#!/usr/bin/bash
declare -a array=(1,2,3,4,5); #配列
declare -i nElems=5; #要素の数
##
# <>exec()
# forの一重ループ
function exec(){
local key=$1;
for((i=0;i<nElems;i++)){
if(( array[i]==key ));then
echo "key : $key";
fi
}
}
##
#
# 実行
exec 3;
O(N^2)
バブルソートがこれに該当する
かけ算の九九がこのパターン。
二重ループに代表される縦と横、iとj、XとYといった総当り探索がこれ。
二重ループ構造なので「指数的爆発」が起きて非常に遅くなる。
データが多いとクラッシュする可能性もあるので注意。
O(N) に比べてかなり遅い。
#!/usr/bin/bash
declare -a array=(1 2 3 4 5); #配列
declare -i nElems=5;
##
# <>exec()
# forの二重ループ
function exec(){
for((i=0;i<nElems;i++)){
for((j=0;j<nElems;j++)){
echo $(( array[i] + array[j] ));
}
}
}
exec ;
O(N^3)
行列乗算の以下のパターン
とてつもなく遅いです。
for((i=0;i<n;i++)){
for((j=0;j<n;j++)){
for((k=0;k<n;k++)){
array[k]=$(( array[i] * array[j] ));
O(log(N))
二分探索法(バイナリサーチ)がこれに該当する。
処理するたびにターゲットが絞られて早くなるオーダー
O(N) に比べてかなり早い
データ量に対して、計算量を常に半分にしていくのですごく速い。
プログラムで書かれているのは「二分探索」というアルゴリズム。
データ量が 4000 あっても 12 回の処理で完了する
#!/usr/bin/bash
#########
# バイナリサーチによる
# ユーザーへのインタフェース
#########
#
# 画面をクリアする
clear
# 要素の数は100
declare -i nElems=100;
echo "要素の数は $nElems です。"
#
for((i=0;i<nElems;i++)){
arr[$i]=$i;
echo "${arr[$i]}";
}
#
echo -n "探したい数字を入力してください:"
read item
##
declare -i lb=1;
declare -i ub=$nElems;
while [ $lb -le $ub ];do
x=`expr $ub + $lb`
mid=`expr $x / 2`
if [ $item -lt ${arr[$mid]} ];then
ub=`expr $mid - 1`
elif [ $item -gt ${arr[$mid]} ];then
lb=`expr $mid + 1`
elif [ $item -eq ${arr[$mid]} ];then
echo $item found at position $mid
break
fi
done
if [ $lb -gt $ub ];then
echo not found;
fi
O(N log(N))
クイックソート、マージソートがこれに該当する。
ビッグオーとアルゴリズム「ざっくり比較」
| 表記 | 意味 | 例 | 速い順 |
|---|---|---|---|
| O(1) | 定数 | 配列を添字アクセスする場合(ex. a[0] = 1;) | 1 |
| O(log(n)) | 対数 | 二分探索 | 2 |
| O(n) | 一時 | 線形探索、グラフ探索 | 3 |
| O(n log n) | nlog n | クイックソート、マージソート | 4 |
| O(N^2) | 二次 | バブルソート、挿入ソート | 5 |
ビッグオー記法についてとても詳しく書かれている奇跡のページ
計算量オーダーの求め方を総整理! 〜 どこから log が出て来るか 〜
配列の基本操作で学ぶ「追加」
例題1
以下の配列の追加に必要な操作(回)数を求めると

次のように行われ、検索数5回、追加1回、合計は6回です。

例題2
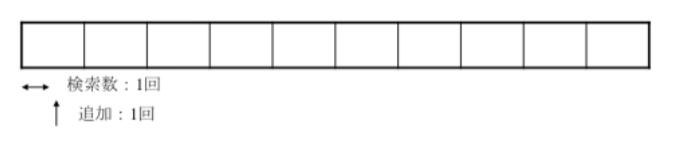
以下の配列の追加に必要な操作(回)数を求めると

次のように行われるため、検索数1回、追加で1回の合計2回となります。
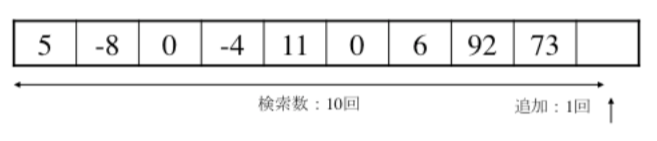
例題3
以下の配列の追加に必要な操作(回)数を求めると

次のように行われる。 検索数は10回、追加で1回。
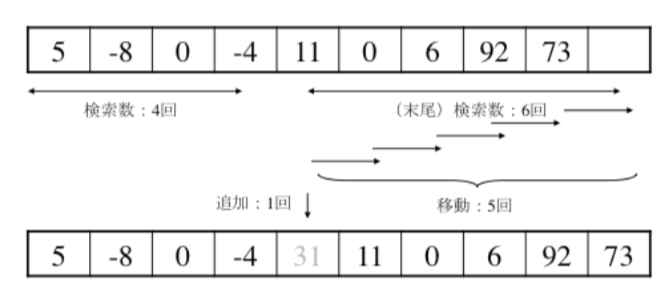
例題4
以下の配列の4の後ろに31を追加したい。
この追加(挿入)に必要な操作(回)数を求めると、

次のように行われる。
まず、−4を検索します(場所を特定して記憶します)。
次に配列の末尾に空いているセル(場所)があるか否かを調べます。
あると、−4のセル以降のセルの後方への移動が可能となります(空きセルがないと、追加(挿入)は不可能となります)。
−4を検索するために4回、その場所から、末尾に空いているセルがあるか否かを調べるために6回、これで検索数は10回となります。
その後、空白セルに一つずつセルを移動します。この作業は目印(−4の次のセル)まで行われます。この移動回数が5回となります。
そうすると、セルに空きが生まれたので追加で1回。
操作回数の合計は16回となります。
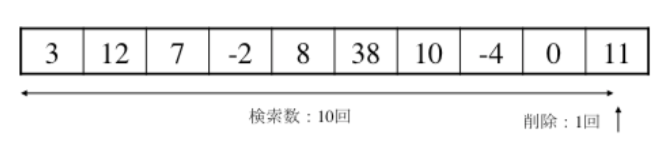
配列の基本操作で学ぶ「削除」
例題5
以下の配列の11の要素を削除したい。この削除に必要な操作(回)数を求めると、

次のように行われる。
該当のデータは最後の要素に格納されているため、配列の先頭から10回の検索が必要です。データが見つかったため、削除自体は最後に1回行われます。つまり合計操作回数は11回となります。
最後のデータを削除すると、作業は検索と削除しか含めませんが、その他の一の削除になると、移動の作業も必要となります。
例題6
以下の配列のセル8の内容を削除したい。この削除に必要な操作回数を求めると、

次のように行われる。
該当のデータの削除後、空白のセルが生じます。配列にはこれは許されないため、その位置から以降の内容のあるセルの移動が必要となります。
まず8を検索し、5回の検索で見つかりました。
その後、8を削除し操作が1回。
8の場所が空いたため、その位置以降の要素の内容を移動します。移動対象は5つなので、移動操作は5回行われます。
つまり合計操作回数は11回となります。

配列の基本操作で学ぶ「存在確認」
例題7
以下の配列に7のデータがあるかを確認したい。

次のように行われる。
配列がからっぽなので検索は1回。このため操作回数は1回となります。

例題8
以下の配列に7のデータがあるかを確認したい。この検索に必要な操作(回)数を求めると、

次のように行われる。
該当データがないことと、最後のセルしか空いていないため、配列を最後まで検索する必要があります。結果は検索が10回となります。

- ヒント
- ビッグ・オーという計算量の割合を表す記法があるということを覚えておいてください。
- バブルソートやバイナリサーチがどういった計算量なのかを考えるための基準は、配列へのアクセス方法、いわゆるループの構造です。
- アルゴリズムの全てにビッグオーがあります。
- この章で紹介した後半の「挿入」「削除」「移動」といった動きが計算量に影響するということを覚えておくと良いでしょう。
「ざっくり」シリーズのご紹介
【アルゴリズム 再帰】ざっくりわかるシェルスクリプト15
https://suzukiiichiro.github.io/posts/2022-10-07-01-algorithm-recursion-suzuki/
【アルゴリズム キュー】ざっくりわかるシェルスクリプト14
https://suzukiiichiro.github.io/posts/2022-10-06-01-algorithm-queue-suzuki/
【アルゴリズム スタック】ざっくりわかるシェルスクリプト13
https://suzukiiichiro.github.io/posts/2022-10-06-01-algorithm-stack-suzuki/
【アルゴリズム 挿入ソート】ざっくりわかるシェルスクリプト12
https://suzukiiichiro.github.io/posts/2022-10-05-01-algorithm-insertionsort-suzuki/
【アルゴリズム 選択ソート】ざっくりわかるシェルスクリプト11
https://suzukiiichiro.github.io/posts/2022-10-05-01-algorithm-selectionsort-suzuki/
【アルゴリズム バブルソート】ざっくりわかるシェルスクリプト10
https://suzukiiichiro.github.io/posts/2022-10-05-01-algorithm-bubblesort-suzuki/
【アルゴリズム ビッグオー】ざっくりわかるシェルスクリプト9
https://suzukiiichiro.github.io/posts/2022-10-04-01-algorithm-bigo-suzuki/
【アルゴリズム 2次元配列編】ざっくりわかるシェルスクリプト8
https://suzukiiichiro.github.io/posts/2022-10-03-01-algorithm-eval-array-suzuki/
【アルゴリズム 配列準備編】ざっくりわかるシェルスクリプト7
https://suzukiiichiro.github.io/posts/2022-10-03-01-algorithm-array-suzuki/
【アルゴリズム 配列編】ざっくりわかるシェルスクリプト6
https://suzukiiichiro.github.io/posts/2022-09-27-01-array-suzuki/
【grep/sed/awkも】ざっくりわかるシェルスクリプト5
https://suzukiiichiro.github.io/posts/2022-02-02-01-suzuki/
【grep特集】ざっくりわかるシェルスクリプト4
https://suzukiiichiro.github.io/posts/2022-01-24-01-suzuki/
【はじめから】ざっくりわかるシェルスクリプト3
https://suzukiiichiro.github.io/posts/2022-01-13-01-suzuki/
【はじめから】ざっくりわかるシェルスクリプト2
https://suzukiiichiro.github.io/posts/2022-01-12-01-suzuki/
【はじめから】ざっくりわかるシェルスクリプト1
https://suzukiiichiro.github.io/posts/2022-01-07-01-suzuki/
【TIPS】ざっくりわかるシェルスクリプト
https://suzukiiichiro.github.io/posts/2022-09-26-01-tips-suzuki/


