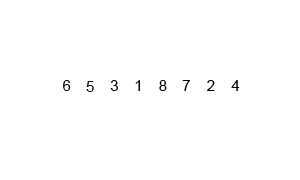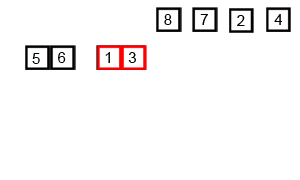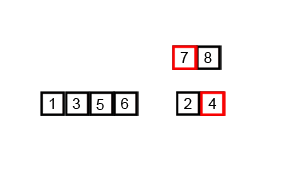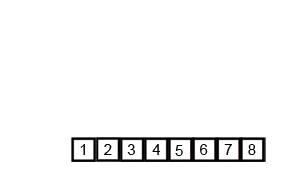マージソート
マージソートは、これまで紹介した「バブルソート」「挿入ソート」「選択ソート」と比べると、少なくともスピードの点ではずっと高速で効率的です。
マージソートの効率
「バブルソート」「挿入ソート」「選択ソート」がO(N^2)の時間を要するのに対し、マージソートはO(N*log(N))です。
例えば、N(ソートする項目の数)が10,000の場合、N^2 は100,000,000ですが、N*log(N)は40,000です。
別の言い方をすると、マージソートで40秒を要するソートは、挿入ソートでは約28時間かかります。
プログラムの構成は、今後出てくるクイックソートやシェルソートよりもわかりやすく、構築が容易です。
マージソートの欠点
マージソートの欠点は、ソートする配列と同じサイズの配列をもう一つ必要とすることです。
元の配列がかろうじてメモリ内に収まるという大きさだったら、マージソートは使えません。
しかし、メモリに余裕がある場合は、マージソートは良い選択です。
マージソートのアルゴリズム
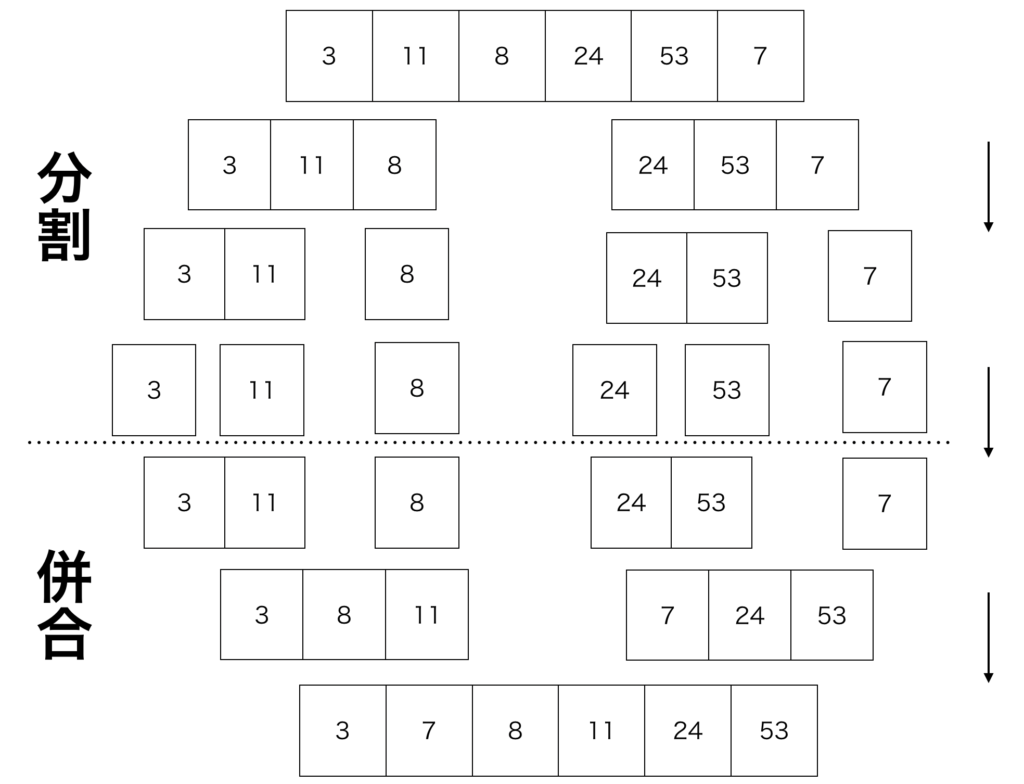
マージソートのアルゴリズムの中心は、未ソート配列を要素の数が2以下になるまで分解を繰り返し、1つないし2つの要素を比較、並べ替えを行いながらマージ(併合)を繰り返します。
要素列を均等に分割できる場合のマージソート
要素列の要素数が偶数個ある場合は分割は真ん中で行われます。
要素列の要素数がが奇数個の場合、たとえば要素列の要素数が7つの場合、2で割った部分(3ですね)と残り(4)というふうに分割します。
ここでは、要素列の要素数が偶数個の場合を考えていきます。
分割後左側の「分解」処理
1.並べ替える前の未ソート列があります。これをこれからマージソートで並べ替えます。
2.まずは未ソート列を2つに分割します。
3.分割した2つの未ソート列を要素の数が2以下になるまで分割を繰り返します。(ここではあっというまに2以下となりました)
4.分割した要素を比較するため6と3に分解しました。
分割後左側の「マージ」処理
5.6と3を比較して並べ替えと同時にマージ(併合)します。これにより(3,6)となりました。
6.7と5も比較するために7と5に分解します。
7.7と5に分解した要素を比較して並べ替えます。ここでは並べ替える必要はないようでした。
8.(3,6)と(5,7)の4つの要素を比較して並べ替えながらマージ(併合)します。
分割後右側の「分解」処理
9.右側(2,8,4,1)を分解して(2,8)と(4,1)に分解します。
10.2と8を更に分解し、比較できるように分解します。
11.2と8を比較して(2,8)とマージしました。ここでは並び順に変更はないようでした。
12.4と1も比較できるように分解します。
分割後右側の「マージ」処理
13.分解した4と1を比較して並べ替えを行いつつ(1,4)とマージします。
14.(2,8)と(1,4)の4つの要素を比較しながらマージします。
15.(3,5,6,7)と(1,2,4,8)を比較しながらマージします。
- ヒント
- 分割段階では要素の数が2以下となるまで分割を繰り返し、マージは、最初は1つ、次は2つの要素を組み合わせて4つとし、次は4つの要素をもつ2つのソート済み列をマージして8つの要素をもつソート済み列を組み上げていきます。
要素列を均等に分割できない場合のマージソート
要素列の要素数が偶数個ある場合は分割は真ん中で行われます。
要素列の要素数がが奇数個の場合、たとえば要素列の要素数が7つの場合、2で割った部分(3ですね)と残り(4)というふうに分割します。
ここでは、要素列の要素数が奇数個の場合を考えていきます。
この図では、動作を左右2つに分けて表しています。
左側は分割、右側はマージ(併合)です。
まずは、左側から説明します。
前半の左側の説明
7つの要素があります。
7つの要素は真ん中で半分に分けることができません。
そのため3つ(5,4,2)と4つ(8,7,3,6)に分割しています。
2つに分けたら、(5,4,2)をさらに2つに分けます。
先程同様、3つの要素は真ん中で半分に分けることができません。
ですので、(5)と(4,2)で2つに分けます。
ここが重要なのですが、分解した要素の数が2以下になるまでこれらの動作を繰り返します。
そこで、左側の一番下の図の通り、要素の大小が比較できる直前までを行い準備を完了とします。
後半の右側の説明
後半右側の図は下から処理を進めていきます。
マージソートは、マージ(併合)するたびに並べ替えを行います。
右側一番下の段から二段目に上がる段階で、それぞれの大小を比較して並べ替えを行いマージ(併合)します。
4と2を比較して(2,4)と並べ替えてマージ。
8と7を比較して(7,8)と並べ替えてマージ。
3と6を比較して(3,6)と並べ替えて・・・というかそのままマージします。
右側下から2段目から下から3段目の説明ですが、
5と(2,4)を並べ替えてマージします。
これまでは2つの要素を比較してマージしましたが、ここからの比較・マージの対象となる要素は少しずつ増えます。
(7,8)と(3,6)の4つの要素を比較して小さな要素から順番に並べ替えながらマージします。
右側下から3段目の様子になったら、(2,4,5)と(3,6,7,8)の7つの要素を比較して小さな要素から順番に並べ替えてマージします。
- ヒント
- 左側上から2段目の未ソートの要素を並べ替えるよりも、右側下から3段目(上から2段め)の要素列を並べ替えるほうが断然効率的なのです。
- 理由は、2つの未ソート配列を並べ替えるのと、2つのソート済み配列をマージ(併合)する処理の違いは、要素の比較や交換・移動が、未ソート配列をマージするよりも少なくてすむからです。
- 2つのソート済み配列をマージ(併合)する場合は、2つのソート済み配列先頭の大小を比較しながらマージすれば良いからなのですね。
- マージソートの唯一の欠点は、もとの配列と同じサイズの配列をもう一つ用意する必要があることで、メモリ使用領域が2倍必要ということです。
プログラムソース
この章で使っているプログラムソースは以下にあります。
05_1MergeSort.sh マージソート
マージソートのアルゴリズム
マージソートのプログラムは、
- mergeSort()
- merge()
の2つの部分から構成されています。
まず、配列全体を指定した mergeSort() を呼び出します。
mergeSort()は配列を要素の数が2以下になるまで分割を繰り返すので再帰関数となります。
その後、merge()により2つの済み配列の比較・並べかえを行いながら「マージ(併合)」を繰り返し、1つのソート済み配列を作ります。
配列の 𝑙 番目から 𝑟 番目までをソートする merge_sort(arr[], l, r) のアルゴリズムは以下のようになります。
𝑚𝑖𝑑=(𝑙+𝑟)/2 とする
merge_sort(𝑎𝑟𝑟[],𝑙,𝑚𝑖𝑑) で 𝑙 番目から 𝑚𝑖𝑑 番目までソート
merge_sort(𝑎𝑟𝑟[],𝑚𝑖𝑑+1,𝑟) で 𝑚𝑖𝑑+1 番目から 𝑟 番目までソート
merge(𝑎𝑟𝑟[],𝑙,𝑚𝑖𝑑,𝑟) で先程ソートした配列をマージしながらソート
mergeSort(){
local lowerBound="$1" ;
local upperBound="$2" ;
#範囲が1なら再帰呼び出しの終了 基底条件
if [ "$lowerBound" -eq "$upperBound" ]; then
#ソートは不要
:
else
#列を2つに分割する中間点を見つける
local mid=$(( ($lowerBound+$upperBound) / 2 ));
#前半分をソート
mergeSort "$lowerBound" "$mid" ;
#後半分をソート
mergeSort "$(($mid+1))" "$upperBound"
#両者をマージ
mergeSortLogic "$lowerBound" "$(($mid+1))" "$upperBound" ;
fi
}
merge() を実行する時点で、mergeSort( 部分配列の前半 ) と mergeSort( 部分配列の後半 ) の処理はすでに終了しています。
merge はすでにソートされている部分配列の前半と後半に対して実行されます。
言い換えれば、merge の役割は、すでにソートされている2つの部分配列を1つのソートされた部分配列にすることです。
merge(){
#作業スペースのインデクス
local j=0;
#下半分の部分配列が始まる位置
local lowPtr="$1" ;
#上半分の部分配列が始まる位置
local highPtr="$2" ;
#上半分の配列の上限位置
local _upperBound="$3" ;
#下半分の配列の上限位置
local _lowerBound="$lowPtr" ;
local _mid="$(($highPtr-1))" ;
#項目の数
local n="$(($_upperBound-$_lowerBound+1))" ;
#マージする列が2つある場合
while (("$lowPtr" <= "$_mid" && "$highPtr" <= "$_upperBound" ));do
#小さい値をコピー
if [ "${array[$lowPtr]}" -lt "${array[$highPtr]}" ]; then
workArray[$j]="${array[((lowPtr++))]}" ;
((j++)) ;
else
workArray[$j]="${array[((highPtr++))]}" ;
((j++)) ;
fi
done
#前半分のリスト
while (( "$lowPtr" <= "$_mid" )); do
#前半分の要素をそのまま作業用配列にコピー
workArray[$j]="${array[((lowPtr++))]}" ;
((j++)) ;
done
#後半分のリスト
while (( "$highPtr" <= "$_upperBound" )) ; do
#後半分の要素を逆順に作業用配列にコピー
workArray[$j]="${array[((highPtr++))]}" ;
((j++)) ;
done
#昇順に整列するよう1つのリストにまとめる
#作業用配列の両端から取り出したデータをマージして配列に入れる
for((j=0; j<$n; j++)); do
array[$(($_lowerBound+$j))]="${workArray[$j]}" ;
done
}
マージ(併合)のロジック

上の図は、merge()のメカニズムをカードの操作で表します。
左右にカードの束があり、各束のカードは小さい順に整列されているものとします。
merge()の処理は、各カードの山の一番上にあるカードの値を比較し、小さい方を選択して順番に並べます。
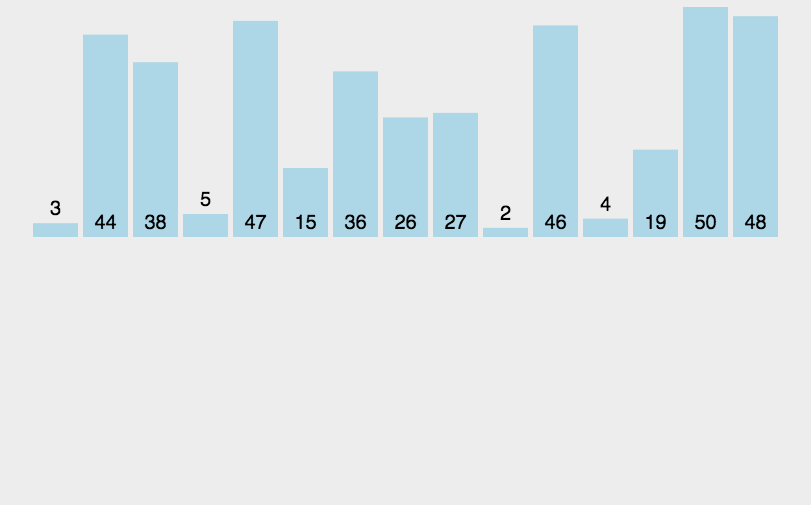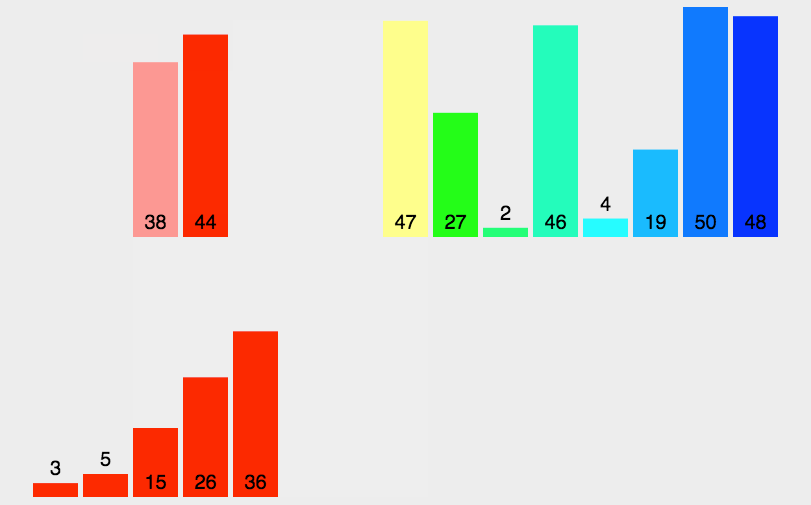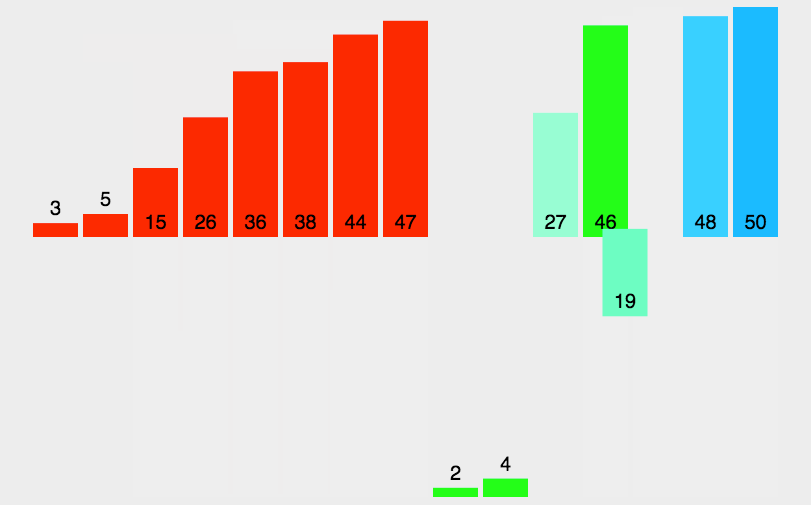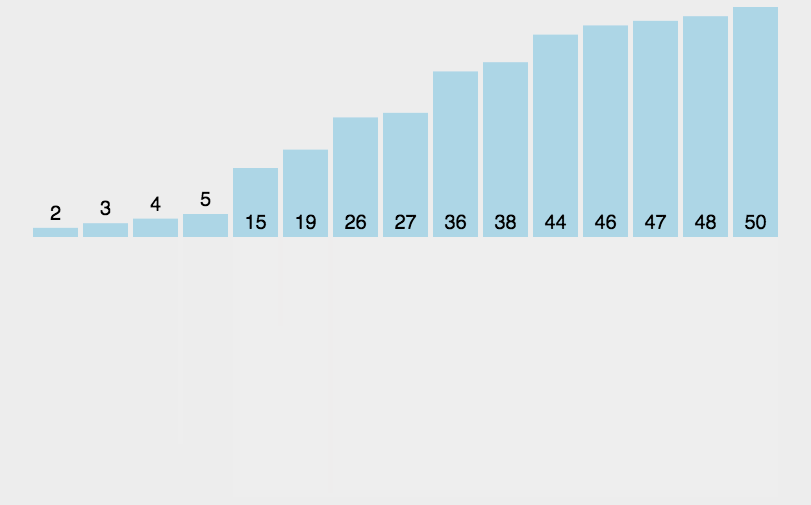
要素16のマージソート
要素が増えてもマージソートのロジックは全く変わりません。
複数の要素を真ん中で2つに分け分解を繰り返し、その後併合も繰り返します。
こうしたアルゴリズムを「分割統治法」といいます。
要素が大量の場合のマージソート
要素の数が大きくなった場合も分割統治法により、怯える必要がないのです。
分割を再帰により繰り返し、併合を繰り返します。
マージソートの計算量
-
時間計算量(time complexity)
最悪・平均・最善の計算時間は O(N* log(N))となります。これはO(N2)と比べると非常に高速です。 -
領域計算量 (space complexity)
merge() 関数は、配列の長さ Nのオーダーで新しいメモリが必要となってしまいます。
これにより消費メモリはO(N)となります。
マージソートの効率
では、これまでどおり、ソートの効率をグラフにプロットしたものです。参考にしてください。

各ソート比較
bash/シェルスクリプトによる疑似2次元配列の実装
#!/bin/bash
#######################################
# 05_1MergeSort.shを、少しだけオブジェクティブに
# aRray[0].getValue() で値を取得できるように改変した
# 配列にIDと値を入れるだけのbashスクリプト
#######################################
##
# グローバル変数
declare -i nElems=0;
declare -i wElems=0;
#
# <>display()
# 配列を表示
function display(){
for((i=0;i<nElems;i++)){
echo -n "aRray[$i] \
ID: " $( aRray[$i].getID ) " \
Value:" $( aRray[$i].getValue ) ;
echo "";
}
}
##
# <>setWvalue()
# セッター
function setWvalue() {
#今後挿入や置き換えに備えてnElemsとは別の変数を用意しておく
local Welem="$1";
local wvalue="$2";
eval "wRray[$Welem].getWvalue() { echo "$wvalue"; }"
}
##
# <>setWiD()
# セッター
function setWID(){
#今後挿入や置き換えに備えてnElemsとは別の変数を用意しておく
local Welem="$1";
local wid="$2";
eval "wRray[$Welem].getWID() { echo "$wid"; }"
}
##
# <>setValue()
# セッター
function setValue() {
#今後挿入や置き換えに備えてnElemsとは別の変数を用意しておく
local Elem="$1";
local value="$2";
eval "aRray[$Elem].getValue() { echo "$value"; }"
}
##
# <>setID()
# セッター
function setID(){
#今後挿入や置き換えに備えてnElemsとは別の変数を用意しておく
local Elem="$1";
local ID="$2";
eval "aRray[$Elem].getID() { echo "$ID"; }"
}
##
# <> insert
# 配列の要素に値を代入
function insert(){
local ID=$1; #100からの連番
local value=$2; #配列に代入される要素の値
setID "$nElems" "$ID"; #IDをセット
setValue "$nElems" "$value"; #Valueをセット
((nElems++));
}
##
# <> set Array
# 配列を作成
function setArray(){
local N=$1; #すべての要素数
local ID=100; #100からの連番
local value; #配列に代入される要素の値
for((i=0;i<N;i++)){
value=$( echo $RANDOM );
insert $((ID++)) $value;
}
}
##
# <>bubbleSort()
# バブルソート
# URL:https://www.youtube.com/watch?v=xli_FI7CuzA
function bubbleSort(){
local tmp_id;
local tmp_value;
for((i=nElems;i>0;i--)){
for((j=0;j<i-1;j++)){
if(($(aRray[$j].getValue)>$(aRray[$((j+1))].getValue)));then
# 交換
tmp_id=$(aRray[$j].getID);
tmp_value=$(aRray[$j].getValue);
setID "$j" $(aRray[$((j+1))].getID); #IDをセット
setValue "$j" $(aRray[$((j+1))].getValue); #Valueをセット
setID $((j+1)) $tmp_id; #IDをセット
setValue $((j+1)) $tmp_value; #Valueをセット
# 交換
fi
}
}
}
## <>selectionSort()
# 選択ソート
# URL:https://www.youtube.com/watch?v=g-PGLbMth_g
function selectionSort(){
local tmp_id;
local tmp_value;
for((i=0;i<nElems;i++)){
min=$i;
for((j=i+1;j<nElems;j++)){
if(($(aRray[$min].getValue)>$(aRray[$j].getValue)));then
min=$j;
fi
}
# 交換
tmp_id=$(aRray[$min].getID);
tmp_value=$(aRray[$min].getValue);
setID "$min" $(aRray[$i].getID); #IDをセット
setValue "$min" $(aRray[$i].getValue); #Valueをセット
setID $i $tmp_id; #IDをセット
setValue $i $tmp_value; #Valueをセット
# 交換
}
}
##
## <>insertionSort()
# 挿入ソート
# URL:https://www.youtube.com/watch?v=DFG-XuyPYUQ
function insertionSort(){
local tmp_id;
local tmp_value;
for((out=1;out<nElems;out++)){
tmp_id=$(aRray[$out].getID);
tmp_value=$(aRray[$out].getValue);
in=$out;
while (( in > 0 ))&&(( $(aRray[$((in-1))].getValue) > tmp_value ));do
setID "$in" $(aRray[$((in-1))].getID); #IDをセット
setValue "$in" $(aRray[$((in-1))].getValue); #Valueをセット
in=$((in-1));
done
setID "$in" $tmp_id; #IDをセット
setValue "$in" $tmp_value; #Valueをセット
}
}
##
# merge()
# マージソートのマージ(併合)部分メソッド
merge(){
#作業スペースのインデクス
local j=0;
#下半分の部分配列が始まる位置
local lowPtr="$1" ;
#上半分の部分配列が始まる位置
local highPtr="$2" ;
#上半分の配列の上限位置
local _upperBound="$3" ;
#下半分の配列の上限位置
local _lowerBound="$lowPtr" ;
local _mid="$(($highPtr-1))" ;
#項目の数
local n="$((_upperBound-_lowerBound+1))" ;
#マージする列が2つある場合
while (("$lowPtr" <= "$_mid" && "$highPtr" <= "$_upperBound" ));do
#小さい値をコピー
if (($(aRray[$lowPtr].getValue)<$(aRray[$highPtr].getValue)));then
setWID "$j" $(aRray[$lowPtr].getID); #IDをセット
setWvalue "$j" $(aRray[$lowPtr].getValue); #Valueをセット
((lowPtr++));
((j++)) ;
else
setWID "$j" $(aRray[$highPtr].getID); #IDをセット
setWvalue "$j" $(aRray[$highPtr].getValue); #Valueをセット
((highPtr++));
((j++)) ;
fi
done
#前半分のリスト
while (( "$lowPtr" <= "$_mid" )); do
#前半分の要素をそのまま作業用配列にコピー
setWID "$j" $(aRray[$lowPtr].getID); #IDをセット
setWvalue "$j" $(aRray[$lowPtr].getValue); #Valueをセット
((lowPtr++));
((j++)) ;
done
#後半分のリスト
while (( "$highPtr" <= "$_upperBound" )) ; do
#後半分の要素を逆順に作業用配列にコピー
setWID "$j" $(aRray[$highPtr].getID); #IDをセット
setWvalue "$j" $(aRray[$highPtr].getValue); #Valueをセット
((highPtr++));
((j++)) ;
done
#昇順に整列するよう1つのリストにまとめる
#作業用配列の両端から取り出したデータをマージして配列に入れる
for((j=0; j<$n; j++)); do
setID $((_lowerBound+j)) $(wRray[$j].getWID); #IDをセット
setValue $((_lowerBound+j)) $(wRray[$j].getWvalue); #Valueをセット
done
}
## <>mergeSort()
# マージソート
# URL:https://www.youtube.com/watch?v=4VqmGXwpLqc
mergeSort(){
local lowerBound="$1" ;
local upperBound="$2" ;
#範囲が1なら再帰呼び出しの終了 基底条件
if [ "$lowerBound" -eq "$upperBound" ]; then
#ソートは不要
:
else
#列を2つに分割する中間点を見つける
local mid=$(( $((lowerBound+upperBound)) / 2 ));
#前半分をソート
mergeSort "$lowerBound" "$mid" ;
#後半分をソート
mergeSort "$((mid+1))" "$upperBound"
#両者をマージ
merge "$lowerBound" "$((mid+1))" "$upperBound" ;
fi
}
# <>execSort()
# メインルーチン
function execSort(){
local N=$1;
setArray $N; #配列をセット
echo "修正前"
display;
#bubbleSort; #バブルソート
#selectionSort; #選択ソート
#insertionSort; #挿入ソート
mergeSort 0 "$(($nElems-1))" ; #マージソート
echo "修正後"
display;
}
##
# 実行
time execSort 10;
exit;
実行結果
bash-5.1$ bash 05_1Eval_MergeSort.sh
修正前
aRray[0] ID: 100 Value: 3114
aRray[1] ID: 101 Value: 16112
aRray[2] ID: 102 Value: 28827
aRray[3] ID: 103 Value: 32104
aRray[4] ID: 104 Value: 11076
aRray[5] ID: 105 Value: 7824
aRray[6] ID: 106 Value: 450
aRray[7] ID: 107 Value: 21013
aRray[8] ID: 108 Value: 28555
aRray[9] ID: 109 Value: 3675
修正後
aRray[0] ID: 106 Value: 450
aRray[1] ID: 100 Value: 3114
aRray[2] ID: 109 Value: 3675
aRray[3] ID: 105 Value: 7824
aRray[4] ID: 104 Value: 11076
aRray[5] ID: 101 Value: 16112
aRray[6] ID: 107 Value: 21013
aRray[7] ID: 108 Value: 28555
aRray[8] ID: 102 Value: 28827
aRray[9] ID: 103 Value: 32104
real 0m0.287s
user 0m0.123s
sys 0m0.163s
bash-5.1$
「ざっくり」シリーズのご紹介
【アルゴリズム マージソート】ざっくりわかるシェルスクリプト17
https://suzukiiichiro.github.io/2022-10-19-01-mergesort-suzuki/
【アルゴリズム 連結リスト】ざっくりわかるシェルスクリプト16
https://suzukiiichiro.github.io/posts/2022-10-18-01-list-suzuki/
【アルゴリズム 再帰】ざっくりわかるシェルスクリプト15
https://suzukiiichiro.github.io/posts/2022-10-07-01-algorithm-recursion-suzuki/
【アルゴリズム キュー】ざっくりわかるシェルスクリプト14
https://suzukiiichiro.github.io/posts/2022-10-06-01-algorithm-queue-suzuki/
【アルゴリズム スタック】ざっくりわかるシェルスクリプト13
https://suzukiiichiro.github.io/posts/2022-10-06-01-algorithm-stack-suzuki/
【アルゴリズム 挿入ソート】ざっくりわかるシェルスクリプト12
https://suzukiiichiro.github.io/posts/2022-10-05-01-algorithm-insertionsort-suzuki/
【アルゴリズム 選択ソート】ざっくりわかるシェルスクリプト11
https://suzukiiichiro.github.io/posts/2022-10-05-01-algorithm-selectionsort-suzuki/
【アルゴリズム バブルソート】ざっくりわかるシェルスクリプト10
https://suzukiiichiro.github.io/posts/2022-10-05-01-algorithm-bubblesort-suzuki/
【アルゴリズム ビッグオー】ざっくりわかるシェルスクリプト9
https://suzukiiichiro.github.io/posts/2022-10-04-01-algorithm-bigo-suzuki/
【アルゴリズム 2次元配列編】ざっくりわかるシェルスクリプト8
https://suzukiiichiro.github.io/posts/2022-10-03-01-algorithm-eval-array-suzuki/
【アルゴリズム 配列準備編】ざっくりわかるシェルスクリプト7
https://suzukiiichiro.github.io/posts/2022-10-03-01-algorithm-array-suzuki/
【アルゴリズム 配列編】ざっくりわかるシェルスクリプト6
https://suzukiiichiro.github.io/posts/2022-09-27-01-array-suzuki/
【grep/sed/awkも】ざっくりわかるシェルスクリプト5
https://suzukiiichiro.github.io/posts/2022-02-02-01-suzuki/
【grep特集】ざっくりわかるシェルスクリプト4
https://suzukiiichiro.github.io/posts/2022-01-24-01-suzuki/
【はじめから】ざっくりわかるシェルスクリプト3
https://suzukiiichiro.github.io/posts/2022-01-13-01-suzuki/
【はじめから】ざっくりわかるシェルスクリプト2
https://suzukiiichiro.github.io/posts/2022-01-12-01-suzuki/
【はじめから】ざっくりわかるシェルスクリプト1
https://suzukiiichiro.github.io/posts/2022-01-07-01-suzuki/
【TIPS】ざっくりわかるシェルスクリプト
https://suzukiiichiro.github.io/posts/2022-09-26-01-tips-suzuki/