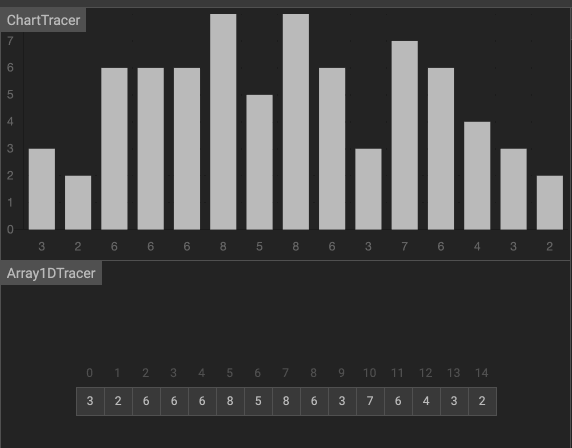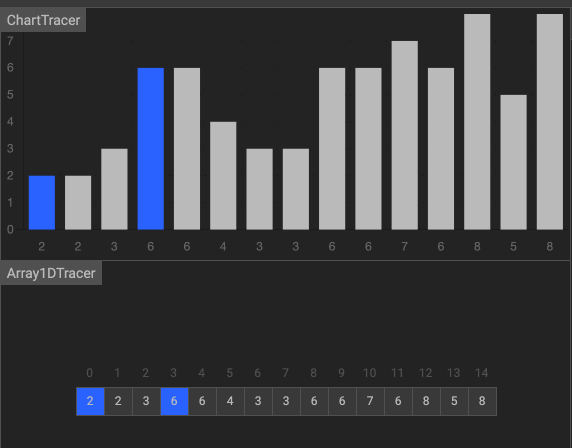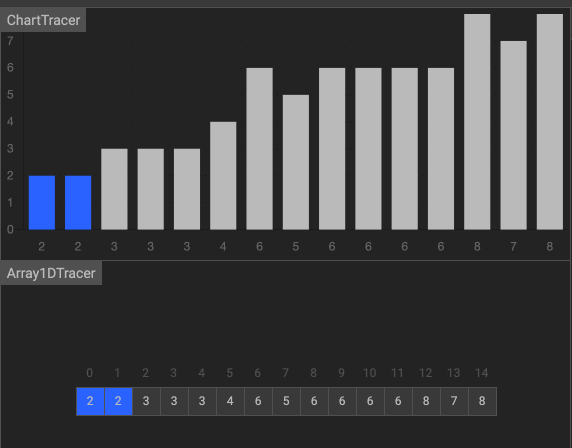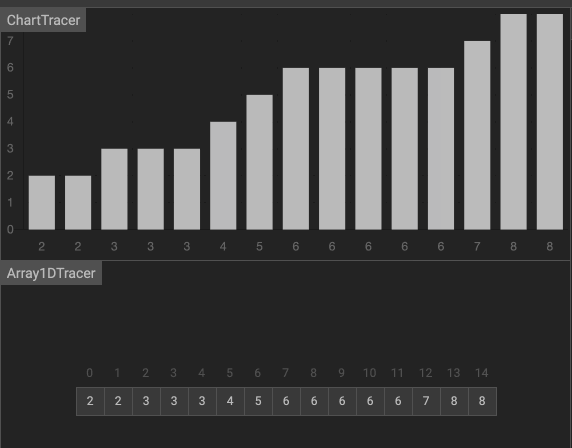
【アルゴリズム ソート比較】ざっくりわかるシェルスクリプト２０

#!/bin/bash

##########################################
# Bash(シェルスクリプト)で学ぶ
# アルゴリズムとデータ構造  
#          一般社団法人共同通信社情報技術局
#   鈴木維一郎(suzuki.iichiro@kyodonews.jp)
#
#
# ステップバイステップでアルゴリズムを学ぶ
# 
# 目次
#   ソートアルゴリズム
#   バブルソート
#   選択ソート
#   挿入ソート
#   マージソート
#   シェルソート
#   クイックソート
#
##########################################
##
# display()
# 共通部分
function display(){
  for((i=0;i<nElems;i++)){
    echo "$i" "${array[i]}";
  }
  echo "-----";
}
##
# insert()
# 配列を作成
function insert(){
  array[nElems++]="$1";
}
##
# setArray()
# 配列をセット
function setArray(){
  nElems=0;
  for((i=0;i<$1;i++)){
    insert $(echo "$RANDOM");
  }
}
#
#############################################
# 1. バブルソート 13404mm
# https://ja.wikipedia.org/wiki/バブルソート
# https://www.youtube.com/watch?v=8Kp-8OGwphY
#   平均計算時間が O(N^2)
#   安定ソート
#   比較回数は「  n(n-1)/2  」
#   交換回数は「  n^2/2  」
#   派生系としてシェーカーソートやコムソート
##
function bubbleSort(){
  local i j t;# t:temp
  for((i=nElems;i>0;i--)){
    for((j=0;j<i-1;j++)){
      ((array[j]>array[j+1]))&&{
        t="${array[j]}";
        array[j]="${array[j+1]}";
        array[j+1]="$t";
      }
    }
  }
}
#
##########################################
# 選択ソート 3294mm
# https://ja.wikipedia.org/wiki/選択ソート
# https://www.youtube.com/watch?v=f8hXR_Hvybo
#   平均計算時間が O(N^2)
#   安定ソートではない
#   比較回数は「  n(n-1)/2  」
#   交換回数は「  n-1  」
##
# selectionSort()
# 選択ソート
function selectionSort(){
  local i j t m;# t:temp m:min
  for((i=0;i<nElems;i++)){
    m="$i";
    for((j=i+1;j<nElems;j++)){
      ((array[m]>array[j]))&& m="$j";
    }
    ((m==i))&& continue;
    t="${array[m]}";
    array[m]="${array[i]}";
    array[i]="$t";
  }
}
#
##########################################
# 挿入ソート 3511mm
# https://ja.wikipedia.org/wiki/挿入ソート
# https://www.youtube.com/watch?v=DFG-XuyPYUQ
#   平均計算時間が O(N^2)
#   安定ソート
#   比較回数は「  n(n-1)/2以下  」
#   交換回数は「  約n^2/2以下  」
## 
# insertionSort()
# 挿入ソート
function insertionSort(){
  local o i t;# o:out i:in t:temp
  for((o=1;o<nElems;o++)){
    t="${array[o]}";
    for((i=o;i>0&&array[i-1]>t;i--)){
      array[i]="${array[i-1]}";
    }
    array[i]="$t";
  }
}
#
#############################################
# マージソート 1085mm
# https://ja.wikipedia.org/wiki/マージソート
# https://www.youtube.com/watch?v=EeQ8pwjQxTM
#   平均計算時間が O(N(Log N))
#   安定ソート
#   50以下は挿入ソート、5万以下はマージソート、
#   あとはクイックソートがおすすめ。
#   バブルソート、挿入ソート、選択ソートがO(N^2)の
#   時間を要するのに対し、マージ
#   ソートはO(N*logN)です。
#   例えば、N(ソートする項目の数）が10,000ですと、
#   N^2は100,000,000ですが、
#   n*logNは40,000です。
#   別の言い方をすると、マージソートで４０秒を
#   要するソートは、挿入ソートでは約２８時間かかります。
#   マージソートの欠点は、ソートする配列と同サイズ
#   の配列をもう一つ必要とする事です。
#   元の配列がかろうじてメモリに治まるという大きさ
#   だったら、マージソートは使えません。
##
# mergeSortLogic()
# 
function mergeSortLogic(){
  local f=$1 m=$2 l=$3;# f:first m:mid l:last w:workArray
  local n i j n1;
  ((n=l-f+1));
  for((i=f,j=0;i<=l;)){
    w[j++]="${array[i++]}";
  }
  ((m>l))&&((m=(f+l)/2));
  ((n1=m-f+1));
  for((i=f,j=0,k=n1;i<=l;i++)){
    {
      ((j<n1))&&{
        ((k==n))||{ 
          ((${w[j]}<${w[k]}))
        }
      }
    }&&{ 
      array[i]="${w[j++]}";
    }||{
      array[i]="${w[k++]}";
    }
  }
}
##
# mergeSort()
# マージソート
function mergeSort(){
    local f="$1" l="$2" m=;# f:first l:last m:mid
    ((l>f))||return 0;
    m=$(((f+l)/2));
    mergeSort "$f" "$m";
    mergeSort "$((m+1))" "$l"
    mergeSortLogic "$f" "$m" "$l";
}
#
###############################################
# シェルソート 1052mm
# https://ja.wikipedia.org/wiki/シェルソート
# https://www.youtube.com/watch?v=M9YCh-ZeC7Y
#   平均計算時間が O(N((log N)/(log log N))^2)
#   安定ソートではない
#   挿入ソート改造版
#   ３倍して１を足すという処理を要素を越えるまで行う
##
# shellSort()
# シェルソート
function shellSort(){
  local s=1 in t;#s:shell in:inner t:temp
  while((s<nElems/3));do
      s=$((s*3+1));
  done
  while((s>0));do
    for((i=s;i<nElems;i++)){
      t="${array[i]}";
      in="$i";
      while((in>s-1&&array[in-s]>=t));do
        array[in]="${array[in-s]}";
        in=$((in-s));
      done
      array[in]="$t";
    }
    s=$(((s-1)/3));
  done
}
#
###############################################
# クイックソート 1131mm
# https://ja.wikipedia.org/wiki/クイックソート
# https://www.youtube.com/watch?v=aQiWF4E8flQ
#   平均計算時間が O(n Log n)
#   安定ソートではない
#   最大計算時間が O(n^2)
# データ数が 50 以下なら挿入ソート (Insertion Sort)
# データ数が 5 万以下ならマージソート (Merge Sort)
# データ数がそれより多いならクイックソート (Quick Sort)
##
# quickSort()
# クイックソート
function quickSort(){
  local -i l r m p t i j k;#r:right l:left m:middle p:part t:temp 
  ((l=i=$1,r=j=$2,m=(l+r)/2));
  p="${array[m]}";
  while((j>i));do
    while [[ 1 ]];do
      ((array[i]<p))&&((i++))||break;
    done
    while [[ 1 ]];do
      ((array[j]>p))&&((j--))||break;
    done
    ((i<=j))&&{
      t="${array[i]}";
      array[i]="${array[j]}";
      array[j]="$t";
      ((i++,j--));
    }
  done
  ((l<j)) && quickSort $l $j;
  ((r>i)) && quickSort $i $r;
}
##
# 実行メソッド
##
function SortCase(){
  setArray $1;
#  display;
  case "$2" in
    bubbleSort) 
      bubbleSort;;
    selectionSort) 
      selectionSort;;
    insertionSort) 
      insertionSort;;
    mergeSort) 
      mergeSort 0 $((nElems-1));;
    shellSort) 
      shellSort;;
    quickSort) 
      quickSort 0 $((nElems-1));;
  esac
#  display;
}
##
# ソート各種
# 必要であればコメントアウトなどしてください。
function Sort(){
  echo -n "bubbleSort";
  time SortCase 1000 "bubbleSort";
  echo "";
  echo -n "selectionSort";
  time SortCase 1000 "selectionSort";
  echo "";
  echo -n "insertionSort";
  time SortCase 1000 "insertionSort";
  echo "";
  echo -n "mergeSort";
  time SortCase 1000 "mergeSort";
  echo "";
  echo -n "shellSort";
  time SortCase 1000 "shellSort";
  echo "";
  echo -n "quickSort";
  time SortCase 1000 "quickSort";
  echo "";
}
##
# メイン
Sort;
exit;