Nクイーン問題とは
Nクイーン問題とは、「8列×8行のチェスボードに8個のクイーンを、互いに効きが当たらないように並べよ」というエイトクイーン問題のクイーンの数を N として、どこまで大きなNまで解を求めることができるかという問題で、「Nクイーン問題」とも言う。

Nクイーン問題は、1848年から存在し、ガウスなど著名な科学者が研究した工学研究の頂点となる研究である。
名前の通り8つのクイーンの解を求めるというパズルであり、Nクイーンは、エイトクイーンの拡張版で、Nの値は8、9、10,11,12・・・と言った風に増え続け、そのNの値であるボードの解を求めるものである。
クイーンとは、チェスで使われているクイーンを指し、チェス盤の中で、縦、横、斜めにどこまでも進むことができる駒で、日本の将棋でいう「飛車と角」を合わせた動きとなる。
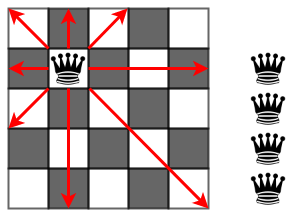
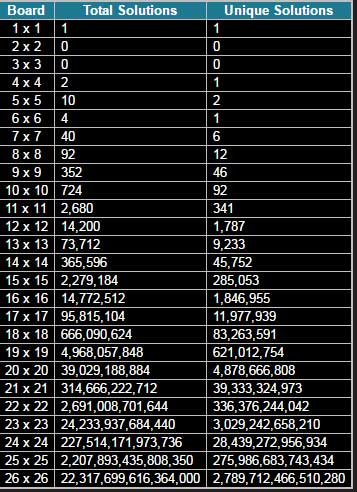
8列×8行で構成される一般的なチェスボードにおける8クイーン問題の解は、解の総数は92個である。
比較的単純な問題なので、大学の学部レベル演習問題として取り上げられることが多い。

8クイーン問題程度であれば、人力またはプログラムによる「力まかせ探索」でも解を求めることができるが、
Nが大きくなると解が一気に爆発し、実用的な時間では解けなくなる。

そもそものエイトクイーン問題の歴史について
「エイト・クイーン」は1848年にチェスプレイヤーのマックス・ベッツェルによって提案されたパズル。
8×8マスのチェス盤の上に、縦横と斜め方向にどこまででも進めるという駒・クイーンを8個並べるというもの。
「どの駒も他の駒に取られるような位置に置いてはいけない」というルールが設定されている。

このルールに従った場合、いくつの正解が存在するのか、長らくの間にわたって謎とされていた。
考案から100年以上が経過した1874年、Guntherが行列式を用いて解く方法を提案し、イギリスのグレイシャー(Glaisher)によってNが8の場合の全解(基本解)が「12個」であることを確認した。
この問題は、チェス盤の一辺のマスの数とクイーンの数を同一にしたNクイーン問題とも呼ばれており、Nの数が増えるに連れて飛躍的にその解数が増大することが知られている。
すべての解が判明!?
全ての解が判明しているのは、2009年にドレスデン工科大学で計算された「26クイーン」で、その基本解は2789兆7124億6651万289個、転回形などのバリエーション解を含めると、その数は2京2317兆6996億1636万4044個にもなることがわかっています。
その後、同、ドレスデン工科大学は、2016年に「27クイーン」を解決した。

セント・アンドルーズ大学のコンピューターサイエンティストであるIan Gent博士らによる研究チームは、この「Nクイーン問題」から派生する「Nクイーン穴埋め問題」(n-Queens Completion)パズルの複雑性に関する(PDF http://jair.org/media/5512/live-5512-10126-jair.pdf)論文を作成しています。
Complexity of n-Queens Completion
https://www-users.york.ac.uk/~pwn503/n-queens-jair.pdf
解決方法
基本的にこの問題を解決するためにはバックトラック法と呼ばれる、いわば「総当たり法」が用いられる。
全ての選択肢を試すためには、膨大な時間を必要とし、マス(N)が大きくなるに従って増えるクイーンの数によって、その時間は指数関数的に一気に増加する。
Gent氏によると、この「Nクイーン穴埋め問題」を素早く解決できるコンピューターやアルゴリズムの開発が進むことで、我々が日々抱えている問題を解決する技術の進化が期待できるとのこと。
先述のように、現代の科学でも解決できているNクイーン問題は、27×27マスの「27クイーン」にとどまっている。
穴埋め問題であっても、そこから先へと進むためには、現在はまだ存在していない新しい技術を開発することが必須となっている。
P対NP問題
この問題は、2000年にアメリカのクレイ数学研究所が100万ドル(約1億1000万円)の賞金とともに設定したミレニアム懸賞問題の一つに数えられる「P対NP問題」の証明につなが るものとされています。
NP問題
「答えを見つけるのは難しいかもしれないが、答えがあっているかどうかは素早くチェックできる問題」
P問題
「簡単に素早く解ける問題」
「簡単に素早く解けるP問題の答えが合っているかを素早く確認できるNP問題である」ことは証明されている。
その逆、つまり
「答えを素早く確認できるNP問題はすべて素早く解くことができるか?」という問題を証明するというもの。
これを解くためには膨大な量の計算を素早く行うことが必要になり、現代のコンピューター技術でも解決までには数万年の時間が必要になると考えられています。
現在すべての解が判明しているもの
Jeff Somers氏が巧みなビット演算による高速化,上下反転の解を考慮し、探索を半分に削減でN=23
2004年にIntel Pentium 4 Xeon 2.8GHzのプロセッサを68個搭載するPCクラスタで、20日間をかけてn=24を解決した電気通信大学がN=24
2005年にニッツァ大学で N=25
2009年にドレスデン工科大学でN=26
2016年にドレスデン工科大学でN=27
の解を求めることに成功している。
wikipedia: エイト・クイーン問題
https://ja.wikipedia.org/wiki/エイト・クイーン
| N | 達成日時 | 組織名 | 参考情報 |
|---|---|---|---|
| N22 | JSomers | 巧みなビット演算による高速化,上下反転の解を考慮し、探索を半分に削減。Jeff Somers氏がN=23の解を求めるときに使用した解法 | |
| N23 | takaken | JSomers版を高橋謙一郎氏が改良。対称性に着目して代表解のみを探索。再帰呼び出しによるプログラム解毒性の向上。 | |
| N24 | 2004年4月11日 | 電気通信大学 | 2004年4月 68CPU x 22日(1,496 CPU日 N24) JSomers版を改良し、7〜24%の性能向上。電通大でN=24を求めるときに使用した解法 |
| N25 | 2005年6月11日 | ProActive | 2005年5月 185 days 4 hours 54 minutes 52 seconds 854 Java grid computation by INRIA, France Real >6 Months Sequential >53 Years http://www-sop.inria.fr/oasis/ProActive2/apps/nqueens25.html |
| N26 | 2009年7月11日 | tu-dresden | FPGA ( 1 : 822 2.5 GHz-QuadCore systemsに相当(約176 * 4CPU = 704 CPU)) x 240日(168,960 CPU日 N26) 9-month cpmputation of FPGAs completing July 1,2009. Result confirmed by Russian MC# super computing project on August 30,2009. |
| N27 | 2016年 月 日 | tu-dresden | https://github.com/preusser/q27 |
歴史的未解決問題に懸賞金
1000年を超える歴史を持つボードゲーム「チェス」には単なるゲームの勝敗ではなく、そのルールに即したさまざまなパズルの課題「チェス・プロブレム」が存在している。
エイト・クイーンはチェスの駒のうち、8個のクイーンだけを使うパズルなのですが、その規模を大きく拡大して行くと、現代数学における未解決問題となり、1億円の賞金がかかる「P対NP問題」の解明につながるものと考えられている。

歴史あるチェスのパズル問題が現代数学における未解決問題の解明につながる可能性
http://gigazine.net/news/20170905-million-dollar-chess-problem/
Nクイーンは今のコンピュータでは絶対解けない。解けたら1億円もらえるよ
https://www.gizmodo.jp/2017/10/eight-queens-puzzle.html
解けたら賞金1億円! 数学の7つの未解決問題のひとつ「P≠NP」問題へのアプローチがもたらすもの
https://logmi.jp/tech/articles/45330
2017 | “Simple” chess puzzle holds key to $1m prize | University of St Andrews
https://www.st-andrews.ac.uk/news/archive/2017/title,1539813,en.php
Can You Solve the Million-Dollar, Unsolvable Chess Problem? - Atlas Obscura
http://www.atlasobscura.com/articles/queens-puzzle-chess-problem-solution-software
その他の参考リンク
GooleなどWebを探索すると無数のページがあることがわかる。その中でも充実したサイトを紹介したい。
おおよそ以下のサイトをかみしめて読み解けば情報は90%網羅されている。
N-Queens 問題(Nobuhide Tsudaさん)
http://vivi.dyndns.org/tech/puzzle/NQueen.html
Puzzle DE Programming(M.Hiroiさん)
バックトラックとビット演算による高速化
http://www.geocities.jp/m_hiroi/puzzle/nqueens.html
takakenさん(高橋謙一郎さん)のページ
http://www.ic-net.or.jp/home/takaken/nt/queen/index.html
の、みなさんが掲示板で議論している模様(貴重ですね)
http://www2.ic-net.or.jp/~takaken/auto/guest/bbs62.html
ptimal Queens
英語だが、上記の全てがJavaで書かれていて群を抜いている
http://penguin.ewu.edu/~trolfe/Queens/OptQueen.html
その他のリンク
https://rosettacode.org/wiki/N-queens_problem
http://www.cc.kyoto-su.ac.jp/~yamada/ap/backtrack.html
http://yucchi.jp/java/java_tip/n_queens_problem/n_queens_problem.html
http://www.shido.info/py/queen_py3.html
http://toraneko75.sakura.ne.jp/wp/?p=223
http://yoshiiz.blog129.fc2.com/blog-entry-380.html
http://nw.tsuda.ac.jp/class/algoB/c6.html
http://www.kawa.net/works/js/8queens/nqueens.html
http://www.yasugi.ai.kyutech.ac.jp/2012/4/nq.html
http://www.neuro.sfc.keio.ac.jp/~masato/jv/nqueen/MPneuron.java
http://fujimura2.fiw-web.net/java/lang/page-20-3.html
https://github.com/pankajmore/DPP/blob/master/EPI/src/puzzles/NQueens.java
http://www.kanadas.com/ccm/queens-sort/index-j.html
http://chiiji.s10.xrea.com/nn/nqueen/nqueenn.shtml
http://www.neuro.sfc.keio.ac.jp/~masato/jv/nqueen/nqueenDemo.htm
さらに参考リンク
N=22発見 JeffSomers
ビットマップを N-Queens に最初に応用したのは Jeff Somers 氏のようだ。
参照:The N Queens Problem
http://www.jsomers.com/nqueen_demo/nqueens.html(リンク切れのようだ)
N=24発見 電気通信大学
2004年、電気通信大学の研究グループが、処理を並列化し
N=24 の解の個数を世界で初めて発見。
http://www.arch.cs.titech.ac.jp/~kise/nq/
プレスリリース
http://www.arch.cs.titech.ac.jp/~kise/nq/press-2004-10-05.txt
電通大が「N-queens」問題の世界記録達成
http://www.itmedia.co.jp/news/articles/0410/06/news079.html
University of North Texas
http://larc.unt.edu/ian/24queens/
NQueens問題 QJHの基本構想は、”部分解から全体解を構成するというアプローチ”(部分解合成法:Parts Assembly Approach)です。
http://deepgreen.game.coocan.jp/NQueens/nqueen_index.htm
N Queens World records
http://www.nqueens.de/sub/WorldRecord.en.html
N=21-23 computed by Sylvain PION (Sylvain.Pion(AT)sophia.inria.fr) and Joel-Yann FOURRE (Joel-Yann.Fourre(AT)ens.fr).
N=24 from Kenji KISE (kis(AT)is.uec.ac.jp), Sep 01 2004
N=25 from Objectweb ProActive INRIA Team (proactive(AT)objectweb.org), Jun 11 2005 [Communicated by Alexandre Di Costanzo (Alexandre.Di_Costanzo(AT)sophia.inria.fr)]. This calculation took about 53 years of CPU time.N=25 has been confirmed by the NTU 25Queen Project at National Taiwan University and Ming Chuan University, led by Yuh-Pyng (Arping) Shieh, Jul 26 2005. This computation took 26613 days CPU time.
N=26 as calculated by Queens(AT)TUD [http://queens.inf.tu-dresden.de/]. - Thomas B. Preußer, Jul 11 2009
N=27 as calculated by the Q27 Project [https://github.com/preusser/q27]. - Thomas B. Preußer, Sep 23 2016
次回は、シェルスクリプトでエイト・クイーンを解決・解説していきたいと思います。
参考リンク
以下の詳細説明を参考にしてください。
【参考リンク】Nクイーン問題 過去記事一覧
【Github】エイト・クイーンのソース置き場 BashもJavaもPythonも!
Nクイーン問題(50)第七章 マルチプロセス Python編
https://suzukiiichiro.github.io/posts/2023-06-21-04-n-queens-suzuki/
Nクイーン問題(49)第七章 マルチスレッド Python編
https://suzukiiichiro.github.io/posts/2023-06-21-03-n-queens-suzuki/
Nクイーン問題(48)第七章 シングルスレッド Python編
https://suzukiiichiro.github.io/posts/2023-06-21-02-n-queens-suzuki/
Nクイーン問題(47)第七章 クラス Python編
https://suzukiiichiro.github.io/posts/2023-06-21-01-n-queens-suzuki/
Nクイーン問題(46)第七章 ステップNの実装 Python編
https://suzukiiichiro.github.io/posts/2023-06-16-02-n-queens-suzuki/
Nクイーン問題(45)第七章 キャリーチェーン Python編
https://suzukiiichiro.github.io/posts/2023-06-16-01-n-queens-suzuki/
Nクイーン問題(44)第七章 対象解除法 Python編
https://suzukiiichiro.github.io/posts/2023-06-14-02-n-queens-suzuki/
Nクイーン問題(43)第七章 ミラー Python編
https://suzukiiichiro.github.io/posts/2023-06-14-01-n-queens-suzuki/
Nクイーン問題(42)第七章 ビットマップ Python編
https://suzukiiichiro.github.io/posts/2023-06-13-05-n-queens-suzuki/
Nクイーン問題(41)第七章 配置フラグ Python編
https://suzukiiichiro.github.io/posts/2023-06-13-04-n-queens-suzuki/
Nクイーン問題(40)第七章 バックトラック Python編
https://suzukiiichiro.github.io/posts/2023-06-13-03-n-queens-suzuki/
Nクイーン問題(39)第七章 バックトラック準備編 Python編
https://suzukiiichiro.github.io/posts/2023-06-13-02-n-queens-suzuki/
Nクイーン問題(38)第七章 ブルートフォース Python編
https://suzukiiichiro.github.io/posts/2023-06-13-01-n-queens-suzuki/
Nクイーン問題(37)第六章 C言語移植 その17 pthread並列処理完成
https://suzukiiichiro.github.io/posts/2023-05-30-17-n-queens-suzuki/
Nクイーン問題(36)第六章 C言語移植 その16 pthreadの実装
https://suzukiiichiro.github.io/posts/2023-05-30-16-n-queens-suzuki/
Nクイーン問題(35)第六章 C言語移植 その15 pthread実装直前版完成
https://suzukiiichiro.github.io/posts/2023-05-30-15-n-queens-suzuki/
Nクイーン問題(34)第六章 C言語移植 その14
https://suzukiiichiro.github.io/posts/2023-05-30-14-n-queens-suzuki/
Nクイーン問題(33)第六章 C言語移植 その13
https://suzukiiichiro.github.io/posts/2023-05-30-13-n-queens-suzuki/
Nクイーン問題(32)第六章 C言語移植 その12
https://suzukiiichiro.github.io/posts/2023-05-30-12-n-queens-suzuki/
Nクイーン問題(31)第六章 C言語移植 その11
https://suzukiiichiro.github.io/posts/2023-05-30-11-n-queens-suzuki/
Nクイーン問題(30)第六章 C言語移植 その10
https://suzukiiichiro.github.io/posts/2023-05-30-10-n-queens-suzuki/
Nクイーン問題(29)第六章 C言語移植 その9
https://suzukiiichiro.github.io/posts/2023-05-30-09-n-queens-suzuki/
Nクイーン問題(28)第六章 C言語移植 その8
https://suzukiiichiro.github.io/posts/2023-05-30-08-n-queens-suzuki/
Nクイーン問題(27)第六章 C言語移植 その7
https://suzukiiichiro.github.io/posts/2023-05-30-07-n-queens-suzuki/
Nクイーン問題(26)第六章 C言語移植 その6
https://suzukiiichiro.github.io/posts/2023-05-30-06-n-queens-suzuki/
Nクイーン問題(25)第六章 C言語移植 その5
https://suzukiiichiro.github.io/posts/2023-05-30-05-n-queens-suzuki/
Nクイーン問題(24)第六章 C言語移植 その4
https://suzukiiichiro.github.io/posts/2023-05-30-04-n-queens-suzuki/
Nクイーン問題(23)第六章 C言語移植 その3
https://suzukiiichiro.github.io/posts/2023-05-30-03-n-queens-suzuki/
Nクイーン問題(22)第六章 C言語移植 その2
https://suzukiiichiro.github.io/posts/2023-05-30-02-n-queens-suzuki/
Nクイーン問題(21)第六章 C言語移植 その1
N-Queens問://suzukiiichiro.github.io/posts/2023-05-30-01-n-queens-suzuki/
Nクイーン問題(20)第五章 並列処理
https://suzukiiichiro.github.io/posts/2023-05-23-02-n-queens-suzuki/
Nクイーン問題(19)第五章 キャリーチェーン
https://suzukiiichiro.github.io/posts/2023-05-23-01-n-queens-suzuki/
Nクイーン問題(18)第四章 エイト・クイーンノスタルジー
https://suzukiiichiro.github.io/posts/2023-04-25-01-n-queens-suzuki/
Nクイーン問題(17)第四章 偉人のソースを読む「N24を発見 Jeff Somers」
https://suzukiiichiro.github.io/posts/2023-04-21-01-n-queens-suzuki/
Nクイーン問題(16)第三章 対象解除法 ソース解説
https://suzukiiichiro.github.io/posts/2023-04-18-01-n-queens-suzuki/
Nクイーン問題(15)第三章 対象解除法 ロジック解説
https://suzukiiichiro.github.io/posts/2023-04-13-02-nqueens-suzuki/
Nクイーン問題(14)第三章 ミラー
https://suzukiiichiro.github.io/posts/2023-04-13-01-nqueens-suzuki/
Nクイーン問題(13)第三章 ビットマップ
https://suzukiiichiro.github.io/posts/2023-04-05-01-nqueens-suzuki/
Nクイーン問題(12)第二章 まとめ
https://suzukiiichiro.github.io/posts/2023-03-17-02-n-queens-suzuki/
Nクイーン問題(11)第二章 配置フラグの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-17-01-n-queens-suzuki/
Nクイーン問題(10)第二章 バックトラックの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-16-01-n-queens-suzuki/
Nクイーン問題(9)第二章 ブルートフォースの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-14-01-n-queens-suzuki/
Nクイーン問題(8)第一章 まとめ
https://suzukiiichiro.github.io/posts/2023-03-09-01-n-queens-suzuki/
Nクイーン問題(7)第一章 ブルートフォース再び
https://suzukiiichiro.github.io/posts/2023-03-08-01-n-queens-suzuki/
Nクイーン問題(6)第一章 配置フラグ
https://suzukiiichiro.github.io/posts/2023-03-07-01-n-queens-suzuki/
Nクイーン問題(5)第一章 進捗表示テーブルの作成
https://suzukiiichiro.github.io/posts/2023-03-06-01-n-queens-suzuki/
Nクイーン問題(4)第一章 バックトラック
https://suzukiiichiro.github.io/posts/2023-02-21-01-n-queens-suzuki/
Nクイーン問題(3)第一章 バックトラック準備編
https://suzukiiichiro.github.io/posts/2023-02-14-03-n-queens-suzuki/
Nクイーン問題(2)第一章 ブルートフォース
https://suzukiiichiro.github.io/posts/2023-02-14-02-n-queens-suzuki/
Nクイーン問題(1)第一章 エイトクイーンについて
https://suzukiiichiro.github.io/posts/2023-02-14-01-n-queens-suzuki/


