第2章 エイトクイーン 配置フラグ
国内で最もきちんと説明していると(僕が勝手に)思っているURLを参照させてください。
僕が説明するよりももっと深みがあります。
(以下上記URLの内容)
前章のバックトラッキング探索では、行の各カラムにクイーンを順に置いてみて、各行に配置しているクイーンの位置と比較してクイーンの効きチェックを行っていた。
が、この処理はfor文で各行を調べていたので、意外と処理が重い。
しかもノードを探索するたびに呼ばれるので、トータルの処理回数が多くなり、それに時間を要する。
そこで、配置可能かどうかを表す配置フラグを事前に用意しておき、それを参照するだけで配置可能かどうかを判定することにする。
フラグをチェックするだけなのでfor文でチェックするよりはるかに高速だ。
チェックするときは高速になるかもしれないが、その配置フラグを更新するのに時間が必を要するのではないかと心配されるかもしれない。
しかし、Nクイーンの場合、各行の配置候補箇所はN箇所なので、N回効きチェックを行う必要があるが、そのための配置フラグはそれ以前の状態で決まるので、更新は1回だけでよい。
つまり、配置フラグの方が処理回数自体が大幅に少なくなり、その結果高速になるということだ。
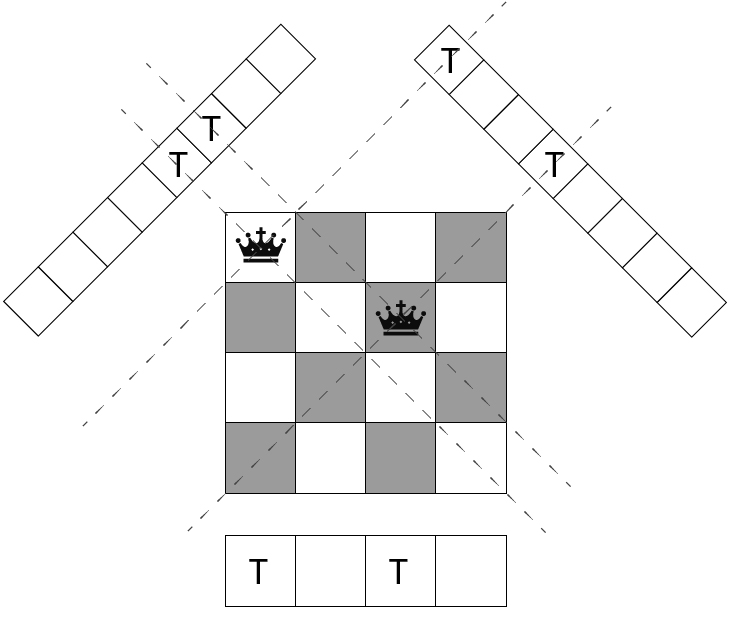
配置フラグとして、垂直・右上・右下方向についてクイーンが配置済みであることを表す
bool 型配列 col[], rup[], rdn[] を用意する(下図参照)。
ほれぼれしますね。
僕は、このページに出会わなかったら、第一章の配置フラグの認識のまま、言い換えればご認識のまま一生を終えていたかもしれません。
「知れば知るほど知らないことを知る」とはよく言ったものです。
第三章で紹介する予定の「ビットマップ」との橋渡しという位置づけの書籍が多いのですが、まだまだこの配置フラグの可能性はあるのではないかと思っています。
なんといっても、ビットマップになると、クイーンの位置を把握するにも、「もう何がなんだかわからなくなる」ので、枝刈りやロジックの最適化に二の足を踏んでしまうのです。
配置フラグ頑張れ!
効き筋のチェック
配置フラグ版では、これまでのブルートフォースやバックトラックで作成した別関数での効き筋チェック関数はありません。
すべて本体関数の中で処理します。
配置フラグ再帰版
配置フラグ再帰版のプログラムソースは以下のとおりです。
: '再帰版配置フラグ';
function rdlFlag_R(){
local -i row="$1";
local -i size="$2";
local -i col=0; # 再帰に必要
if (( row==size ));then
((TOTAL++));
printRecord "$size";# 出力
else
for(( col=0;col<size;col++ )){
board[$row]="$col";
if (( down[col]==0
&& right[row-col+size-1]==0
&& left[row+col]==0));then
down[$col]=1;
right[$row-$col+($size-1)]=1;
left[$row+$col]=1;
rdlFlag_R "$((row+1))" "$size" ;
down[$col]=0;
right[$row-$col+($size-1)]=0;
left[$row+$col]=0;
fi
}
fi
}
配置フラグのロジックについて簡単に説明します。
for(( col=0;col<size;col++ )){
board[$row]="$col";
if (( down[col]==0
&& right[row-col+size-1]==0
&& left[row+col]==0));then
down[$col]=1;
right[$row-$col+($size-1)]=1;
left[$row+$col]=1;
rdlFlag_R "$((row+1))" "$size" ;
down[$col]=0;
right[$row-$col+($size-1)]=0;
left[$row+$col]=0;
fi
}
以下でクイーンを配置します。
board[$row]="$col";
以下の記述は、
if (( down[col]==0
&& right[row-col+size-1]==0
&& left[row+col]==0));then
このように書くこともできます。
明示的に down[col]==0 と書くほうが良いという人もいますし、
if (( down[col]==0
&& right[row-col+size-1]==0
&& left[row+col]==0));then
以下のように書くほうがスッキリするという人もいます。
if (( !down[col]
&& !right[row-col+size-1]
&& !left[row+col]));then
好みです。
以下の部分で、下、右斜下、左斜下を配置済みとして「1」(true)をフラグとしてセットします。
down[$col]=1;
right[$row-$col+($size-1)]=1;
left[$row+$col]=1;
その直後で再帰を実行してrowをインクリメントしながらボードの下方向へクイーンを配置していきます。
rdlFlag_R "$((row+1))" "$size" ;
再帰が終わったら、down[],right[],left[]の配置フラグに「0」を代入してクリアし、空き地にします。
down[$col]=0;
right[$row-$col+($size-1)]=0;
left[$row+$col]=0;
配置フラグ非再帰版
配置フラグ非再帰版のプログラムソースは以下のとおりです。
: '非再帰版配置フラグ(right/down/left flag)';
function rdlFlag_NR(){
local -i row="$1"
local -i size="$2";
local -i matched=0;
for ((i=0;i<size;i++)){ board[$i]=-1; }
while ((row>-1));do
matched=0;
for ((col=board[row]+1;col<size;col++)){
if (( !down[col]
&& !right[col-row+size-1]
&& !left[col+row] ));then
dix=$col;
rix=$((row-col+(size-1)));
lix=$((row+col));
if ((board[row]!=-1));then
down[${board[$row]}]=0;
right[${board[$row]}-$row+($size-1)]=0;
left[${board[$row]}+$row]=0;
fi
board[$row]=$col; # Qを配置
down[$col]=1;
right[$col-$row+($size-1)]=1;
left[$col+$row]=1; # 効き筋とする
matched=1; # 配置した
break;
fi
}
if ((matched));then # 配置済み
((row++)); #次のrowへ
if ((row==size));then
((TOTAL++));
printRecord "$size";# 出力
((row--));
fi
else
if ((board[row]!=-1));then
down[${board[$row]}]=0;
right[${board[$row]}-$row+($size-1)]=0;
left[${board[$row]}+$row]=0;
board[$row]=-1;
fi
((row--)); # バックトラック
fi
done
}
プログラムソース
再帰版・非再帰版を含むすべてのプログラムソースは以下のとおりです。
プログラムソース最下部で、再帰と非再帰の実行をコメントアウトで切り替えてます。
#!/usr/bin/bash
declare -i TOTAL=0; # カウンター
#
: 'ボードレイアウトを出力';
function printRecord(){
size="$1";
echo "$TOTAL";
sEcho=" ";
for((i=0;i<size;i++)){
sEcho="${sEcho}${board[i]} ";
}
echo "$sEcho";
echo -n "+";
for((i=0;i<size;i++)){
echo -n "-";
if((i<(size-1)));then
echo -n "+";
fi
}
echo "+";
for((i=0;i<size;i++)){
echo -n "|";
for((j=0;j<size;j++)){
if((i==board[j]));then
echo -n "O";
else
echo -n " ";
fi
if((j<(size-1)));then
echo -n "|";
fi
}
echo "|";
if((i<(size-1)));then
echo -n "+";
for((j=0;j<size;j++)){
echo -n "-";
if((j<(size-1)));then
echo -n "+";
fi
}
echo "+";
fi
}
echo -n "+";
for((i=0;i<size;i++)){
echo -n "-";
if((i<(size-1)));then
echo -n "+";
fi
}
echo "+";
echo "";
}
#
: '非再帰版配置フラグ(right/down/left flag)';
function rdlFlag_NR(){
local -i row="$1"
local -i size="$2";
local -i matched=0;
for ((i=0;i<size;i++)){ board[$i]=-1; }
while ((row>-1));do
matched=0;
for ((col=board[row]+1;col<size;col++)){
if (( !down[col]
&& !right[col-row+size-1]
&& !left[col+row] ));then
dix=$col;
rix=$((row-col+(size-1)));
lix=$((row+col));
if ((board[row]!=-1));then
down[${board[$row]}]=0;
right[${board[$row]}-$row+($size-1)]=0;
left[${board[$row]}+$row]=0;
fi
board[$row]=$col; # Qを配置
down[$col]=1;
right[$col-$row+($size-1)]=1;
left[$col+$row]=1; # 効き筋とする
matched=1; # 配置した
break;
fi
}
if ((matched));then # 配置済み
((row++)); #次のrowへ
if ((row==size));then
((TOTAL++));
printRecord "$size";# 出力
((row--));
fi
else
if ((board[row]!=-1));then
down[${board[$row]}]=0;
right[${board[$row]}-$row+($size-1)]=0;
left[${board[$row]}+$row]=0;
board[$row]=-1;
fi
((row--)); # バックトラック
fi
done
}
#
#
: '再帰版配置フラグ';
function rdlFlag_R(){
local -i row="$1";
local -i size="$2";
local -i col=0; # 再帰に必要
if (( row==size ));then
((TOTAL++));
printRecord "$size";# 出力
else
for(( col=0;col<size;col++ )){
board[$row]="$col";
if (( down[col]==0
&& right[row-col+size-1]==0
&& left[row+col]==0));then
down[$col]=1;
right[$row-$col+($size-1)]=1;
left[$row+$col]=1;
rdlFlag_R "$((row+1))" "$size" ;
down[$col]=0;
right[$row-$col+($size-1)]=0;
left[$row+$col]=0;
fi
}
fi
}
# 非再帰版配置フラグ
# time rdlFlag_NR 0 5;
#
# 再帰版配置フラグ
time rdlFlag_R 0 5;
#
exit;
実行結果
実行結果は以下の通りです。
bash-3.2$ bash rdlFlag.sh
1
0 2 4 1 3
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
2
0 3 1 4 2
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
3
1 3 0 2 4
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
4
1 4 2 0 3
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
5
2 0 3 1 4
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
6
2 4 1 3 0
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
7
3 0 2 4 1
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
8
3 1 4 2 0
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
9
4 1 3 0 2
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
10
4 2 0 3 1
+-+-+-+-+-+
| | |O| | |
+-+-+-+-+-+
| | | | |O|
+-+-+-+-+-+
| |O| | | |
+-+-+-+-+-+
| | | |O| |
+-+-+-+-+-+
|O| | | | |
+-+-+-+-+-+
bash-3.2$
ブルートフォースとバックトラック、配置フラグの特色と違い
ブルートフォース版
for文で各行の何col目にクイーンを配置するかを決め、最後まで配置した場合は、check_bluteForce() を呼んで、効きであるかどうかを判定し、効きでなければ「解を発見した」として ((TOTAL++))で、解個数をインクリメントしています。
if ((row==size));then
check_bluteForce "$size";
if (( $?==1 ));then
((TOTAL++));
printRecord "$size"; # 出力しないならコメント
fi
else
#for(( col=0;col<(size-row);col++ )){
for(( col=0;col<size;col++ )){
board["$row"]="$col";
bluteForce_R $((row+1)) $size ;
}
fi
バックトラック版
ブルートフォース(力まかせ探索)のように最後まで配置して効きをチェックするのではなく、各行にクイーンを置くたびに効きチェックを行って、効きがあればその状態からの探索を行わない点が異なります。
if ((row==size));then
((TOTAL++));
printRecord "$size"; # 出力
else
for(( col=0;col<size;col++ )){
board["$row"]="$col";
check_backTracking "$row";
if (($?==1));then
backTracking_R $((row+1)) $size ;
fi
}
fi
配置フラグ版
計算済みの配置フラグは再帰によって「メモ」化されます。
この仕組みを利用して、down[],right[],left[] の3つの配列に1は配置済み、0は未配置(クリア)といった情報を与えます。
これにより再帰処理の中で、垂直下方向・対角線左右斜め方向にクイーンが配置済みかどうかをチェックすることが可能です。
どの方向にも配置済みで「なければ」、クイーンを配置し、次の col に進むというわけです。
配置フラグはバックトラックよりもさらに高速です。
for(( col=0;col<size;col++ )){
board[$row]="$col";
if (( down[col]==0
&& right[row-col+size-1]==0
&& left[row+col]==0));then
down[$col]=1;
right[$row-$col+($size-1)]=1;
left[$row+$col]=1;
rdlFlag_R "$((row+1))" "$size" ;
down[$col]=0;
right[$row-$col+($size-1)]=0;
left[$row+$col]=0;
fi
}
参考リンク
以下の詳細説明を参考にしてください。
【参考リンク】Nクイーン問題 過去記事一覧
【Github】エイト・クイーンのソース置き場 BashもJavaもPythonも!
Nクイーン問題(50)第七章 マルチプロセス Python編
https://suzukiiichiro.github.io/posts/2023-06-21-04-n-queens-suzuki/
Nクイーン問題(49)第七章 マルチスレッド Python編
https://suzukiiichiro.github.io/posts/2023-06-21-03-n-queens-suzuki/
Nクイーン問題(48)第七章 シングルスレッド Python編
https://suzukiiichiro.github.io/posts/2023-06-21-02-n-queens-suzuki/
Nクイーン問題(47)第七章 クラス Python編
https://suzukiiichiro.github.io/posts/2023-06-21-01-n-queens-suzuki/
Nクイーン問題(46)第七章 ステップNの実装 Python編
https://suzukiiichiro.github.io/posts/2023-06-16-02-n-queens-suzuki/
Nクイーン問題(45)第七章 キャリーチェーン Python編
https://suzukiiichiro.github.io/posts/2023-06-16-01-n-queens-suzuki/
Nクイーン問題(44)第七章 対象解除法 Python編
https://suzukiiichiro.github.io/posts/2023-06-14-02-n-queens-suzuki/
Nクイーン問題(43)第七章 ミラー Python編
https://suzukiiichiro.github.io/posts/2023-06-14-01-n-queens-suzuki/
Nクイーン問題(42)第七章 ビットマップ Python編
https://suzukiiichiro.github.io/posts/2023-06-13-05-n-queens-suzuki/
Nクイーン問題(41)第七章 配置フラグ Python編
https://suzukiiichiro.github.io/posts/2023-06-13-04-n-queens-suzuki/
Nクイーン問題(40)第七章 バックトラック Python編
https://suzukiiichiro.github.io/posts/2023-06-13-03-n-queens-suzuki/
Nクイーン問題(39)第七章 バックトラック準備編 Python編
https://suzukiiichiro.github.io/posts/2023-06-13-02-n-queens-suzuki/
Nクイーン問題(38)第七章 ブルートフォース Python編
https://suzukiiichiro.github.io/posts/2023-06-13-01-n-queens-suzuki/
Nクイーン問題(37)第六章 C言語移植 その17 pthread並列処理完成
https://suzukiiichiro.github.io/posts/2023-05-30-17-n-queens-suzuki/
Nクイーン問題(36)第六章 C言語移植 その16 pthreadの実装
https://suzukiiichiro.github.io/posts/2023-05-30-16-n-queens-suzuki/
Nクイーン問題(35)第六章 C言語移植 その15 pthread実装直前版完成
https://suzukiiichiro.github.io/posts/2023-05-30-15-n-queens-suzuki/
Nクイーン問題(34)第六章 C言語移植 その14
https://suzukiiichiro.github.io/posts/2023-05-30-14-n-queens-suzuki/
Nクイーン問題(33)第六章 C言語移植 その13
https://suzukiiichiro.github.io/posts/2023-05-30-13-n-queens-suzuki/
Nクイーン問題(32)第六章 C言語移植 その12
https://suzukiiichiro.github.io/posts/2023-05-30-12-n-queens-suzuki/
Nクイーン問題(31)第六章 C言語移植 その11
https://suzukiiichiro.github.io/posts/2023-05-30-11-n-queens-suzuki/
Nクイーン問題(30)第六章 C言語移植 その10
https://suzukiiichiro.github.io/posts/2023-05-30-10-n-queens-suzuki/
Nクイーン問題(29)第六章 C言語移植 その9
https://suzukiiichiro.github.io/posts/2023-05-30-09-n-queens-suzuki/
Nクイーン問題(28)第六章 C言語移植 その8
https://suzukiiichiro.github.io/posts/2023-05-30-08-n-queens-suzuki/
Nクイーン問題(27)第六章 C言語移植 その7
https://suzukiiichiro.github.io/posts/2023-05-30-07-n-queens-suzuki/
Nクイーン問題(26)第六章 C言語移植 その6
https://suzukiiichiro.github.io/posts/2023-05-30-06-n-queens-suzuki/
Nクイーン問題(25)第六章 C言語移植 その5
https://suzukiiichiro.github.io/posts/2023-05-30-05-n-queens-suzuki/
Nクイーン問題(24)第六章 C言語移植 その4
https://suzukiiichiro.github.io/posts/2023-05-30-04-n-queens-suzuki/
Nクイーン問題(23)第六章 C言語移植 その3
https://suzukiiichiro.github.io/posts/2023-05-30-03-n-queens-suzuki/
Nクイーン問題(22)第六章 C言語移植 その2
https://suzukiiichiro.github.io/posts/2023-05-30-02-n-queens-suzuki/
Nクイーン問題(21)第六章 C言語移植 その1
N-Queens問://suzukiiichiro.github.io/posts/2023-05-30-01-n-queens-suzuki/
Nクイーン問題(20)第五章 並列処理
https://suzukiiichiro.github.io/posts/2023-05-23-02-n-queens-suzuki/
Nクイーン問題(19)第五章 キャリーチェーン
https://suzukiiichiro.github.io/posts/2023-05-23-01-n-queens-suzuki/
Nクイーン問題(18)第四章 エイト・クイーンノスタルジー
https://suzukiiichiro.github.io/posts/2023-04-25-01-n-queens-suzuki/
Nクイーン問題(17)第四章 偉人のソースを読む「N24を発見 Jeff Somers」
https://suzukiiichiro.github.io/posts/2023-04-21-01-n-queens-suzuki/
Nクイーン問題(16)第三章 対象解除法 ソース解説
https://suzukiiichiro.github.io/posts/2023-04-18-01-n-queens-suzuki/
Nクイーン問題(15)第三章 対象解除法 ロジック解説
https://suzukiiichiro.github.io/posts/2023-04-13-02-nqueens-suzuki/
Nクイーン問題(14)第三章 ミラー
https://suzukiiichiro.github.io/posts/2023-04-13-01-nqueens-suzuki/
Nクイーン問題(13)第三章 ビットマップ
https://suzukiiichiro.github.io/posts/2023-04-05-01-nqueens-suzuki/
Nクイーン問題(12)第二章 まとめ
https://suzukiiichiro.github.io/posts/2023-03-17-02-n-queens-suzuki/
Nクイーン問題(11)第二章 配置フラグの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-17-01-n-queens-suzuki/
Nクイーン問題(10)第二章 バックトラックの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-16-01-n-queens-suzuki/
Nクイーン問題(9)第二章 ブルートフォースの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-14-01-n-queens-suzuki/
Nクイーン問題(8)第一章 まとめ
https://suzukiiichiro.github.io/posts/2023-03-09-01-n-queens-suzuki/
Nクイーン問題(7)第一章 ブルートフォース再び
https://suzukiiichiro.github.io/posts/2023-03-08-01-n-queens-suzuki/
Nクイーン問題(6)第一章 配置フラグ
https://suzukiiichiro.github.io/posts/2023-03-07-01-n-queens-suzuki/
Nクイーン問題(5)第一章 進捗表示テーブルの作成
https://suzukiiichiro.github.io/posts/2023-03-06-01-n-queens-suzuki/
Nクイーン問題(4)第一章 バックトラック
https://suzukiiichiro.github.io/posts/2023-02-21-01-n-queens-suzuki/
Nクイーン問題(3)第一章 バックトラック準備編
https://suzukiiichiro.github.io/posts/2023-02-14-03-n-queens-suzuki/
Nクイーン問題(2)第一章 ブルートフォース
https://suzukiiichiro.github.io/posts/2023-02-14-02-n-queens-suzuki/
Nクイーン問題(1)第一章 エイトクイーンについて
https://suzukiiichiro.github.io/posts/2023-02-14-01-n-queens-suzuki/