Ｎクイーン問題（１４）第三章　ミラー

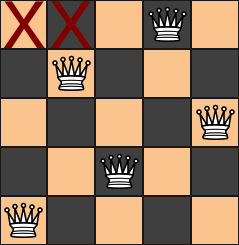
ミラー

ミラー（鏡像）を用いてどのように改善できるのか
Ｎ５＝１０、Ｎ８＝９２といった、N-Queensの解が成立している場合、その鏡像（ミラー）も当然成立していることになります。

左右対称の鏡像の場合この場合は、解がそれぞれ一つずつある。

+-+-+-+-+     +-+-+-+-+  
| | |Q| |     | |Q| | |
+-+-+-+-+     +-+-+-+-+
|Q| | | |     | | | |Q|
+-+-+-+-+     +-+-+-+-+
| | | |Q|     |Q| | | |
+-+-+-+-+     +-+-+-+-+
| |Q| | |     | | |Q| |
+-+-+-+-+     +-+-+-+-+

右の盤面は、左の盤面を左右対称にひっくり返しただけなのに、左盤面の解とは別の解として探索されカウントされます。

左のパターンが発見され１カウントできたら同時に、左右反転させて１カウントすればわざわざ探す必要がなくなります。

左右対称（鏡像）をつかって探索を効率的に進めるにはどうしましょう。

奇数と偶数

Ｎが偶数の場合は、最初の行の右半分、または左半分を除外（無視）すればよいのです。

row0 いわゆる最初の行の左半分には置かない、
言い換えれば、一行目の右半分だけを使って解を探索する。一行目だけですからね！

+-+-+-+-+
|x|x| | |  左側を使わない
+-+-+-+-+
| | | | |
+-+-+-+-+
| | | | |
+-+-+-+-+
| | | | |
+-+-+-+-+

+-+-+-+-+
|x|x| |Q|  右半分を使う
+-+-+-+-+  解があればカウントし、最後にカウントを倍にする。
| | | | |
+-+-+-+-+
| | | | |
+-+-+-+-+
| | | | |
+-+-+-+-+

または

+-+-+-+-+
|x|x|Q| |  右半分を使う
+-+-+-+-+  解があればカウントし、最後にカウントを倍にする。 
| | | | |
+-+-+-+-+
| | | | |
+-+-+-+-+
| | | | |
+-+-+-+-+

Ｎが奇数の場合は、row0（最初の行）の奇数マスを2で割ることができないので、row0（最初の行）のクイーンが真ん中のマスにいない解はすべて、その半分を見つけて2をかければよいのです。

+-+-+-+-+-+        +-+-+-+-+-+  
|x|x| | |Q|        |x|x| |Q| | 中央を除く右側を使う。
+-+-+-+-+-+        +-+-+-+-+-+ 解があればカウントし、最後にカウントを倍にする
| | | | | |        | | | | | |
+-+-+-+-+-+        +-+-+-+-+-+
| | | | | |        | | | | | |
+-+-+-+-+-+        +-+-+-+-+-+
| | | | | |        | | | | | |
+-+-+-+-+-+        +-+-+-+-+-+
| | | | | |        | | | | | |
+-+-+-+-+-+        +-+-+-+-+-+

row0（最初の行）の真ん中のマスにクイーンがあるときも同じことができることが判明しました。

+-+-+-+-+-+
| | |Q| | |  
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+

row0（最初の行）の真ん中のマスにクイーンがある場合、row1（２行目）の真ん中のマスにクイーンがあることはありえません。

+-+-+-+-+-+
| | |Q| | |  
+-+-+-+-+-+
| | |Q| | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+

これで、row1（２行目）のマスのうち、まだ空いているマスは偶数個になりました！
ですので、row1（２行目）の残りのマスの半分を除外すればよいのです。

+-+-+-+-+-+
| | |Q| | |  
+-+-+-+-+-+
|x|x|x| | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+
| | | | | |
+-+-+-+-+-+

これで最初のクイーンが真ん中にある解のちょうど半分を見つけることができます。
これを、最初のクイーンが真ん中にない解の半分と足すと、全解のちょうど半分になり、これを2倍すると、出来上がりです！

図解すると

盤面が偶数の場合は、row0（最初の行）の半分だけを使って、解を倍にする。簡単！
盤面が奇数の場合は、以下を再確認。

row0（１行目）の左半分を除外
奇数Nの場合、これは真ん中のマスまでという意味であり、真ん中のマスは含まれない。このフィルターにより、今回のような解を見つけることができなくなります：

でも大丈夫、その鏡像を求めて、カウントを2倍するのですから：

しかし、これでは、１行目のクイーンが中央のマスにある解をダブルカウントしてしまうことになります。
次の解とその鏡像の解の両方がカウントされることになりますね。
また、1列目の真ん中のマスを除外してしまうと、どちらもカウントされません。
どちらか一方だけをカウントするようにしたいですね。

そこで、２行目の左半分を除外する条件付きフィルタを追加し、このフィルタは１行目のクイーンが真ん中のマスにいるときだけ適用されるようにします。
２行目の真ん中のマスは、最初のクイーンと競合しているので、配置されることを気にする必要はありません。i
最初の行の真ん中にクイーンがある場合は、２行目の中央を除く右半分を使って解の探索し、解があれば２倍すればよいのです。

奇数・偶数共通通過ブロック解説

以下の部分は奇数・偶数に関わらず、いつでも通過するブロックです。
ですので、forの条件は size/2 ということで、盤の半分だけを探索対象とします。

  for ((i=0;i<size/2;i++));do         # 奇数でも偶数でも通過
    bit="$(( 1<<i ))";
    board[0]="$bit";                  # １行目にQを置く
    solve_R "$size" "1" "$((bit<<1))" "$bit" "$((bit>>1))";
  done

奇数ブロック解説

  if ((size%2));then                  # 奇数で通過
    bit=$(( 1<<(size-1)/2 ));
    board[0]=$(( 1<<((size-1)/2) ));  # １行目の中央にQを配置
    local -i left=$(( bit<<1 ));
    local -i down=$(( bit ));
    local -i right=$(( bit>>1 ));
    : '
      if ((size%2));then                #  以下のif文と等価です
        limit="$((size/2-1))";
      else
        limit="$((size/2))";
      fi
    ';
    local -i limit="$(( size%2 ? size/2-1 : size/2 ))";
    for ((i=0;i<limit;i++));do
      bit="$(( 1<<i ))";
      solve_R "$size" "2" "$(( (left|bit)<<1 ))" "$(( down|bit ))" "$(( (right|bit)>>1))";
    done
  fi

これは、、、なんでしょう。

  local -i limit="$(( size%2 ? size/2-1 : size/2 ))";

普通のif文に直すと以下のようになります。

    if ((size%2));then                #  以下のif文と等価です
      limit="$((size/2-1))";
    else
      limit="$((size/2))";
    fi

size%2 は？

bash $ echo $(( 5 % 2 )) 
     $ 1

bash $ echo $(( 6 % 2 )) 
     $ 0

１はtrueで０はfalseなので、奇数であるかどうか？ということになりますね。
ですので、

奇数だったら　limitに size/2-1 を代入
そうでなかったら limitに size/2 を代入　ということになります。

お、ここはなんでしょう。そうです。倍にしているところです。
<<<1 というところがなんだかよくわかりませんが、coolですね。
数を倍にしたいときは、まよわず <<1を使って、難読化していきましょう。

  TOTAL="$(( COUNT2<<1 ))";     # 倍にする

: '再帰版ミラー';
function mirror_R()
{
  local -i size="$1";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit=0; 
  for ((i=0;i<size/2;i++));do         # 奇数でも偶数でも通過
    bit="$(( 1<<i ))";
    board[0]="$bit";                  # １行目にQを置く
    solve_R "$size" "1" "$((bit<<1))" "$bit" "$((bit>>1))";
  done
  if ((size%2));then                  # 奇数で通過
    bit=$(( 1<<(size-1)/2 ));
    board[0]=$(( 1<<((size-1)/2) ));  # １行目の中央にQを配置
    local -i left=$(( bit<<1 ));
    local -i down=$(( bit ));
    local -i right=$(( bit>>1 ));
    : '
      if ((size%2));then                #  以下のif文と等価です
        limit="$((size/2-1))";
      else
        limit="$((size/2))";
      fi
    ';
    local -i limit="$(( size%2 ? size/2-1 : size/2 ))";
    for ((i=0;i<limit;i++));do
      bit="$(( 1<<i ))";
      solve_R "$size" "2" "$(( (left|bit)<<1 ))" "$(( down|bit ))" "$(( (right|bit)>>1))";
    done
  fi
  TOTAL="$(( COUNT2<<1 ))";     # 倍にする
}

ロジック部分解説

実は、ロジック部分は、これまでのビットマップの再帰ソースと同じなのです。
結局、ミラーは偶数であるか、奇数であるかの判別を行っているに過ぎません。
偶数であれば、半分、奇数であれば、中央を除く半分、中央に置かれた場合は、２段めの中央を除く半分を配置可能エリアとして、解があれば２倍にします。

: '再帰版ミラーロジック';
function solve_R()
{
  local -i size="$1";
  local -i row="$2";
  local -i left="$3";
  local -i down="$4";
  local -i right="$5";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit;
  local -i bitmap;
  if (( row==size ));then
    ((COUNT2++));
    printRecord "$size" "1";       # 出力 1:bitmap版 0:それ以外
  else
    # Qが配置可能な位置を表す
    bitmap="$(( mask&~(left|down|right) ))";
    while ((bitmap));do
      bit="$(( -bitmap&bitmap ))"; # 一番右のビットを取り出す
      bitmap="$(( bitmap^bit ))";  # 配置可能なパターンが一つずつ取り出される
      board["$row"]="$bit";        # Qを配置
      solve_R "$size" "$((row+1))" "$(( (left|bit)<<1 ))" "$((down|bit))" "$(( (right|bit)>>1 ))";
    done
  fi
}

ミラー版ソースコード

ソース下部で再帰・非再帰を切換えて実行してください。

#!/usr/bin/bash

declare -i COUNT2=0;
declare -i TOTAL=0;
declare -a board;
declare -i DISPLAY=0;   # ボード出力するか
#
: 'ボードレイアウトを出力 ビットマップ対応版';
function printRecord()
{
  ((TOTAL++));
  size="$1";
  flag="$2"; # bitmap版は1 それ以外は 0
  echo "$TOTAL";
  sEcho=" ";  
  : 'ビットマップ版
     ビットマップ版からは、左から数えます
     上下反転左右対称なので、これまでの上から数える手法と
     rowを下にたどって左から数える方法と解の数に変わりはありません。
     0 2 4 1 3 
    +-+-+-+-+-+
    |O| | | | | 0
    +-+-+-+-+-+
    | | |O| | | 2
    +-+-+-+-+-+
    | | | | |O| 4
    +-+-+-+-+-+
    | |O| | | | 1
    +-+-+-+-+-+
    | | | |O| | 3
    +-+-+-+-+-+
  ';
  if ((flag));then
    local -i i=0;
    local -i j=0;
    for ((i=0;i<size;i++));do
      for ((j=0;j<size;j++));do
       if (( board[i]&1<<j ));then
          sEcho="${sEcho}$((j)) ";
       fi 
      done
    done
  else 
  : 'ビットマップ版以外
     (ブルートフォース、バックトラック、配置フラグ)
     上から数えます
     0 2 4 1 3 
    +-+-+-+-+-+
    |O| | | | |
    +-+-+-+-+-+
    | | | |O| |
    +-+-+-+-+-+
    | |O| | | |
    +-+-+-+-+-+
    | | | | |O|
    +-+-+-+-+-+
    | | |O| | |
    +-+-+-+-+-+

     ';
    local -i i=0;
    for((i=0;i<size;i++)){
      sEcho="${sEcho}${board[i]} ";
    }
  fi
  echo "$sEcho";
  echo -n "+";
  local -i i=0;
  for((i=0;i<size;i++)){
    echo -n "-";
    if((i<(size-1)));then
      echo -n "+";
    fi
  }
  echo "+";
  local -i i=0;
  local -i j=0;
  for((i=0;i<size;i++)){
    echo -n "|";
    for((j=0;j<size;j++)){
      if ((flag));then
        if (( board[i]&1<<j ));then
          echo -n "O";
        else
          echo -n " ";
        fi
      else
        if((i==board[j]));then
          echo -n "O";
        else
          echo -n " ";
        fi
      fi
      if((j<(size-1)));then
        echo -n "|";
      fi
    }
  echo "|";
  if((i<(size-1)));then
    echo -n "+";
    local -i j=0;
    for((j=0;j<size;j++)){
      echo -n "-";
      if((j<(size-1)));then
        echo -n "+";
      fi
    }
  echo "+";
  fi
  }
  echo -n "+";
  local -i i=0;
  for((i=0;i<size;i++)){
    echo -n "-";
    if((i<(size-1)));then
      echo -n "+";
    fi
  }  
  echo "+";
  echo "";
}
#
#
: '非再帰版ミラーロジック';
function solve_NR()
{
  local -i size="$1";
  local -i row="$2";
  local -i mask="$(( (1<<size)-1 ))";
  local -a bitmap[$size];
  local -a left[$size];
  local -a down[$size];
  local -a right[$size];
  local -i bit=0;
  left[$row]="$3";
  down[$row]="$4";
  right[$row]="$5";
  bitmap[$row]=$(( mask&~(left[row]|down[row]|right[row]) ));
  while ((row>0));do
    if (( bitmap[row]>0 ));then
      bit=$(( -bitmap[row]&bitmap[row] ));  # 一番右のビットを取り出す
      bitmap[$row]=$(( bitmap[row]^bit ));  # 配置可能なパターンが一つずつ取り出される
      board[$row]="$bit";                   # Qを配置
      if (( row==(size-1) ));then
        ((COUNT2++));
        printRecord "$size" "1";            # 出力 1:bitmap版 0:それ以外
        ((row--));
      else
        local -i n=$((row++));
        left[$row]=$(((left[n]|bit)<<1));
        down[$row]=$(((down[n]|bit)));
        right[$row]=$(((right[n]|bit)>>1));
        board[$row]="$bit";                 # Qを配置
        # クイーンが配置可能な位置を表す
        bitmap[$row]=$(( mask&~(left[row]|down[row]|right[row]) ));
      fi
    else
      ((row--));
    fi
  done
}
#
: '非再帰版ミラー';
function mirror_NR()
{
  local -i size="$1";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit=0; 
  for ((i=0;i<size/2;i++));do         # 奇数でも偶数でも通過
    bit="$(( 1<<i ))";
    board[0]="$bit";                  # １行目にQを置く
    solve_NR "$size" "1" "$((bit<<1))" "$bit" "$((bit>>1))";
  done
  if ((size%2));then                  # 奇数で通過
    bit=$(( 1<<(size-1)/2 ));
    board[0]=$(( 1<<((size-1)/2) ));  # １行目の中央にQを配置
    local -i left=$(( bit<<1 ));
    local -i down=$(( bit ));
    local -i right=$(( bit>>1 ));
    : '
      if ((size%2));then                #  以下のif文と等価です
        limit="$((size/2-1))";
      else
        limit="$((size/2))";
      fi
    ';
    local -i limit="$(( size%2 ? size/2-1 : size/2 ))";
    for ((i=0;i<limit;i++));do
      bit="$(( 1<<i ))";
      solve_NR "$size" "2" "$(( (left|bit)<<1 ))" "$(( down|bit ))" "$(( (right|bit)>>1))";
    done
  fi
  TOTAL="$(( COUNT2<<1 ))";     # 倍にする
}
#
: '再帰版ミラーロジック';
function solve_R()
{
  local -i size="$1";
  local -i row="$2";
  local -i left="$3";
  local -i down="$4";
  local -i right="$5";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit;
  local -i bitmap;
  if (( row==size ));then
    ((COUNT2++));
    printRecord "$size" "1";       # 出力 1:bitmap版 0:それ以外
  else
    # Qが配置可能な位置を表す
    bitmap="$(( mask&~(left|down|right) ))";
    while ((bitmap));do
      bit="$(( -bitmap&bitmap ))"; # 一番右のビットを取り出す
      bitmap="$(( bitmap^bit ))";  # 配置可能なパターンが一つずつ取り出される
      board["$row"]="$bit";        # Qを配置
      solve_R "$size" "$((row+1))" "$(( (left|bit)<<1 ))" "$((down|bit))" "$(( (right|bit)>>1 ))";
    done
  fi
}
: '再帰版ミラー';
function mirror_R()
{
  local -i size="$1";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit=0; 
  for ((i=0;i<size/2;i++));do         # 奇数でも偶数でも通過
    bit="$(( 1<<i ))";
    board[0]="$bit";                  # １行目にQを置く
    solve_R "$size" "1" "$((bit<<1))" "$bit" "$((bit>>1))";
  done
  if ((size%2));then                  # 奇数で通過
    bit=$(( 1<<(size-1)/2 ));
    board[0]=$(( 1<<((size-1)/2) ));  # １行目の中央にQを配置
    local -i left=$(( bit<<1 ));
    local -i down=$(( bit ));
    local -i right=$(( bit>>1 ));
    : '
      if ((size%2));then                #  以下のif文と等価です
        limit="$((size/2-1))";
      else
        limit="$((size/2))";
      fi
    ';
    local -i limit="$(( size%2 ? size/2-1 : size/2 ))";
    for ((i=0;i<limit;i++));do
      bit="$(( 1<<i ))";
      solve_R "$size" "2" "$(( (left|bit)<<1 ))" "$(( down|bit ))" "$(( (right|bit)>>1))";
    done
  fi
  TOTAL="$(( COUNT2<<1 ))";     # 倍にする
}
#
declare -i size=8;
#
# 再帰版ミラー  
#mirror_R "$size";
#
# 非再帰版ミラー  
 mirror_NR "$size";
# 出力
echo "size: $size" "TOTAL:$TOTAL COUNT2:$COUNT2";

まとめ版のソースコード

こちらは、ブルートフォース、バックトラック、配置フラグ、ビットマップ、ミラーを切り替えて実行できるようになっており、ボードレイアウトの表示や、再帰・非再帰を選択して実行できます。

#!/usr/bin/bash

declare -i COUNT2=0;
declare -i TOTAL=0;     # カウンター
declare -i UNIQUE=0;    # ユニークユーザー
declare -i DISPLAY=0;   # ボード出力するか
#
: 'ボードレイアウトを出力 ビットマップ対応版';
function printRecord()
{
  ((TOTAL++));
  size="$1";
  flag="$2"; # bitmap版は1 それ以外は 0
  echo "$TOTAL";
  sEcho=" ";  
  : 'ビットマップ版
     ビットマップ版からは、左から数えます
     上下反転左右対称なので、これまでの上から数える手法と
     rowを下にたどって左から数える方法と解の数に変わりはありません。
     0 2 4 1 3 
    +-+-+-+-+-+
    |O| | | | | 0
    +-+-+-+-+-+
    | | |O| | | 2
    +-+-+-+-+-+
    | | | | |O| 4
    +-+-+-+-+-+
    | |O| | | | 1
    +-+-+-+-+-+
    | | | |O| | 3
    +-+-+-+-+-+
  ';
  if ((flag));then
    local -i i=0;
    local -i j=0;
    for ((i=0;i<size;i++));do
      for ((j=0;j<size;j++));do
       if (( board[i]&1<<j ));then
          sEcho="${sEcho}$((j)) ";
       fi 
      done
    done
  else 
  : 'ビットマップ版以外
     (ブルートフォース、バックトラック、配置フラグ)
     上から数えます
     0 2 4 1 3 
    +-+-+-+-+-+
    |O| | | | |
    +-+-+-+-+-+
    | | | |O| |
    +-+-+-+-+-+
    | |O| | | |
    +-+-+-+-+-+
    | | | | |O|
    +-+-+-+-+-+
    | | |O| | |
    +-+-+-+-+-+

     ';
    local -i i=0;
    for((i=0;i<size;i++)){
      sEcho="${sEcho}${board[i]} ";
    }
  fi
  echo "$sEcho";
  echo -n "+";
  local -i i=0;
  for((i=0;i<size;i++)){
    echo -n "-";
    if((i<(size-1)));then
      echo -n "+";
    fi
  }
  echo "+";
  local -i i=0;
  local -i j=0;
  for((i=0;i<size;i++)){
    echo -n "|";
    for((j=0;j<size;j++)){
      if ((flag));then
        if (( board[i]&1<<j ));then
          echo -n "O";
        else
          echo -n " ";
        fi
      else
        if((i==board[j]));then
          echo -n "O";
        else
          echo -n " ";
        fi
      fi
      if((j<(size-1)));then
        echo -n "|";
      fi
    }
  echo "|";
  if((i<(size-1)));then
    echo -n "+";
    local -i j=0;
    for((j=0;j<size;j++)){
      echo -n "-";
      if((j<(size-1)));then
        echo -n "+";
      fi
    }
  echo "+";
  fi
  }
  echo -n "+";
  local -i i=0;
  for((i=0;i<size;i++)){
    echo -n "-";
    if((i<(size-1)));then
      echo -n "+";
    fi
  }  
  echo "+";
  echo "";
}
#
: '非再帰版ミラーロジック';
function mirror_solve_NR()
{
  local -i size="$1";
  local -i row="$2";
  local -i mask="$(( (1<<size)-1 ))";
  local -a bitmap[$size];
  local -a left[$size];
  local -a down[$size];
  local -a right[$size];
  local -i bit=0;
  left[$row]="$3";
  down[$row]="$4";
  right[$row]="$5";
  bitmap[$row]=$(( mask&~(left[row]|down[row]|right[row]) ));
  while ((row>-1));do
    if (( bitmap[row]>0 ));then
      bit=$(( -bitmap[row]&bitmap[row] ));  # 一番右のビットを取り出す
      bitmap[$row]=$(( bitmap[row]^bit ));  # 配置可能なパターンが一つずつ取り出される
      board[$row]="$bit";                   # Qを配置
      if (( row==(size-1) ));then
        ((COUNT2++));
        if ((DISPLAY==1));then
          printRecord "$size" "1";            # 出力 1:bitmap版 0:それ以外
        fi
        ((row--));
      else
        local -i n=$((row++));
        left[$row]=$(((left[n]|bit)<<1));
        down[$row]=$(((down[n]|bit)));
        right[$row]=$(((right[n]|bit)>>1));
        board[$row]="$bit";                 # Qを配置
        # クイーンが配置可能な位置を表す
        bitmap[$row]=$(( mask&~(left[row]|down[row]|right[row]) ));
      fi
    else
      ((row--));
    fi
  done
}
#
: '非再帰版ミラー';
function mirror_NR()
{
  local -i size="$1";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit=0; 
  for ((i=0;i<size/2;i++));do         # 奇数でも偶数でも通過
    bit="$(( 1<<i ))";
    board[0]="$bit";                  # １行目にQを置く
    mirror_solve_NR "$size" "1" "$((bit<<1))" "$bit" "$((bit>>1))";
  done
  if ((size%2));then                  # 奇数で通過
    bit=$(( 1<<(size-1)/2 ));
    board[0]=$(( 1<<((size-1)/2) ));  # １行目の中央にQを配置
    local -i left=$(( bit<<1 ));
    local -i down=$(( bit ));
    local -i right=$(( bit>>1 ));
    : '
      if ((size%2));then                #  以下のif文と等価です
        limit="$((size/2-1))";
      else
        limit="$((size/2))";
      fi
    ';
    local -i limit="$(( size%2 ? size/2-1 : size/2 ))";
    for ((i=0;i<limit;i++));do
      bit="$(( 1<<i ))";
      mirror_solve_NR "$size" "2" "$(( (left|bit)<<1 ))" "$(( down|bit ))" "$(( (right|bit)>>1))";
    done
  fi
  TOTAL="$(( COUNT2<<1 ))";     # 倍にする
}
#
: '再帰版ミラーロジック';
function mirror_solve_R()
{
  local -i size="$1";
  local -i row="$2";
  local -i left="$3";
  local -i down="$4";
  local -i right="$5";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit;
  local -i bitmap;
  if (( row==size ));then
    ((COUNT2++));
    if ((DISPLAY));then
      printRecord "$size" "1";       # 出力 1:bitmap版 0:それ以外
    fi
  else
    # Qが配置可能な位置を表す
    bitmap="$(( mask&~(left|down|right) ))";
    while ((bitmap));do
      bit="$(( -bitmap&bitmap ))"; # 一番右のビットを取り出す
      bitmap="$(( bitmap^bit ))";  # 配置可能なパターンが一つずつ取り出される
      board["$row"]="$bit";        # Qを配置
      mirror_solve_R "$size" "$((row+1))" "$(( (left|bit)<<1 ))" "$((down|bit))" "$(( (right|bit)>>1 ))";
    done
  fi
}
#
: '再帰版ミラー';
function mirror_R()
{
  local -i size="$1";
  local -i mask="$(( (1<<size)-1 ))";
  local -i bit=0; 
  for ((i=0;i<size/2;i++));do         # 奇数でも偶数でも通過
    bit="$(( 1<<i ))";
    board[0]="$bit";                  # １行目にQを置く
    mirror_solve_R "$size" "1" "$((bit<<1))" "$bit" "$((bit>>1))";
  done
  if ((size%2));then                  # 奇数で通過
    bit=$(( 1<<(size-1)/2 ));
    board[0]=$(( 1<<((size-1)/2) ));  # １行目の中央にQを配置
    local -i left=$(( bit<<1 ));
    local -i down=$(( bit ));
    local -i right=$(( bit>>1 ));
    : '
      if ((size%2));then                #  以下のif文と等価です
        limit="$((size/2-1))";
      else
        limit="$((size/2))";
      fi
    ';
    local -i limit="$(( size%2 ? size/2-1 : size/2 ))";
    for ((i=0;i<limit;i++));do
      bit="$(( 1<<i ))";
      mirror_solve_R "$size" "2" "$(( (left|bit)<<1 ))" "$(( down|bit ))" "$(( (right|bit)>>1))";
    done
  fi
  TOTAL="$(( COUNT2<<1 ))";     # 倍にする
}
#
: '非再帰版ビットマップ';
function bitmap_NR()
{
  local -i size="$1";
  local -i row="$2";
  local -i mask=$(( (1<<size)-1 ));
  local -a left[$size];
  local -a down[$size];
  local -a right[$size];
  local -a bitmap[$size]
  local -i bitmap[$row]=mask;
  local -i bit=0;
  bitmap[$row]=$(( mask&~(left[row]|down[row]|right[row]) ));
  while ((row>-1));do
    if (( bitmap[row]>0 ));then
      bit=$(( -bitmap[row]&bitmap[row] ));  # 一番右のビットを取り出す
      bitmap[$row]=$(( bitmap[row]^bit ));  # 配置可能なパターンが一つずつ取り出される
      board[$row]="$bit";                   # Qを配置
      if (( row==(size-1) ));then
        ((TOTAL++));
        if ((DISPLAY==1));then
          printRecord "$size" "1";            # 出力 1:bitmap版 0:それ以外
        fi
        ((row--));
      else
        local -i n=$((row++));
        left[$row]=$(((left[n]|bit)<<1));
        down[$row]=$(((down[n]|bit)));
        right[$row]=$(((right[n]|bit)>>1));
        board[$row]="$bit";                 # Qを配置
        # クイーンが配置可能な位置を表す
        bitmap[$row]=$(( mask&~(left[row]|down[row]|right[row]) ));
      fi
    else
      ((row--));
    fi
  done 

}
#
: '再帰版ビットマップ';
function bitmap_R()
{
  local -i size="$1"; 
  local -i row="$2";
  local -i mask="$3";
  local -i left="$4"; 
  local -i down="$5"; 
  local -i right="$6";
  local -i bitmap=;
  local -i bit=;
  local -i col=0;                     # 再帰に必要
  if (( row==size ));then
    ((TOTAL++));
    if ((DISPLAY==1));then
      printRecord "$size" "1";         # 出力 1:bitmap版 0:それ以外
    fi
  else
    bitmap=$(( mask&~(left|down|right) )); # クイーンが配置可能な位置を表す
    while (( bitmap ));do
      bit=$((-bitmap&bitmap)) ;       # 一番右のビットを取り出す
      bitmap=$((bitmap&~bit)) ;       # 配置可能なパターンが一つずつ取り出される
      board[$row]="$bit";             # Qを配置
      bitmap_R "$size" "$((row+1))" "$mask" "$(( (left|bit)<<1 ))" "$((down|bit))" "$(( (right|bit)>>1 ))";
    done
  fi
}
#
: '非再帰版配置フラグ(right/down/left flag)';
function postFlag_NR()
{
  local -i size="$1";
  local -i row="$2"
  local -i matched=0;
  for ((i=0;i<size;i++)){ board[$i]=-1; }
  while ((row>-1));do
    matched=0;
    for ((col=board[row]+1;col<size;col++)){
      if (( !down[col]
        &&  !right[col-row+size-1]
        &&  !left[col+row] ));then
        dix=$col;
        rix=$((row-col+(size-1)));
        lix=$((row+col));
        if ((board[row]!=-1));then
          down[${board[$row]}]=0;
          right[${board[$row]}-$row+($size-1)]=0;
          left[${board[$row]}+$row]=0;
        fi       
        board[$row]=$col;   # Qを配置
        down[$col]=1;
        right[$col-$row+($size-1)]=1;
        left[$col+$row]=1;  # 効き筋とする
        matched=1;          # 配置した
        break;
      fi
    }
    if ((matched));then     # 配置済み
      ((row++));            #次のrowへ
      if ((row==size));then
        ((TOTAL++));
        if ((DISPLAY==1));then
          printRecord "$size";# 出力
        fi
        ((row--));
      fi
    else
      if ((board[row]!=-1));then
        down[${board[$row]}]=0;
        right[${board[$row]}-$row+($size-1)]=0;
        left[${board[$row]}+$row]=0;
        board[$row]=-1;
      fi
      ((row--));            # バックトラック
    fi
  done
}
#
: '再帰版配置フラグ';
function postFlag_R()
{
  local -i size="$1";
  local -i row="$2";
  local -i col=0;       # 再帰に必要
  if (( row==size ));then
     ((TOTAL++));
    if (( DISPLAY==1 ));then
      printRecord "$size";# 出力
    fi
  else
    for(( col=0;col<size;col++ )){
      board[$row]="$col";
      if (( down[col]==0 
        && right[row-col+size-1]==0
        && left[row+col]==0));then
        down[$col]=1;
        right[$row-$col+($size-1)]=1;
        left[$row+$col]=1;
        postFlag_R "$size" "$((row+1))";
        down[$col]=0;
        right[$row-$col+($size-1)]=0;
        left[$row+$col]=0;
      fi
    }
  fi
}
#
: 'バックトラック版効き筋をチェック';
function check_backTracking()
{
  local -i row="$1";
  local -i flag=1;
  for ((i=0;i<row;++i)){
    if (( board[i]>=board[row] ));then
      val=$(( board[i]-board[row] ));
    else
      val=$(( board[row]-board[i] ));
    fi
    if (( board[i]==board[row] || val==(row-i) ));then
      flag=0;
    fi
  }
  [[ $flag -eq 0 ]]
  return $?;
}
#
: '非再帰版バックトラック';
function backTracking_NR()
{
  local -i size="$1";
  local -i row="$2";
  for ((i=0;i<size;i++)){ board[$i]=-1; }
  while ((row>-1));do
    local -i matched=0;
    local -i col=0;  
    for((col=board[row]+1;col<size;col++)){
      board[$row]=$col;
      check_backTracking "$row";  # 効きをチェック
      if (($?==1));then # 直前のreturnを利用
        matched=1;
        break;
      fi
    }
    if ((matched));then
      ((row++));
      if ((row==size));then  # 最下部まで到達
        ((row--));
        ((TOTAL++));
        if (( DISPLAY==1 ));then
          printRecord "$size";# 出力
        fi
      fi
    else
      if ((board[row]!=-1));then
        board[$row]=-1;
      fi
      ((row--));
    fi
 done  
}
#
: '再帰版バックトラック';
function backTracking_R()
{
  local -i size="$1";
  local -i row="$2";
  local -i col=0;
  if ((row==size));then
    ((TOTAL++));
    if (( DISPLAY==1 ));then
      printRecord "$size";# 出力
    fi
  else
    for(( col=0;col<size;col++ )){
      board["$row"]="$col";
      check_backTracking "$row";
      if (($?==1));then 
        backTracking_R  $size $((row+1));
      fi
    }
  fi
}
#
: 'ブルートフォース版効き筋をチェック';
function check_bluteForce()
{
  local -i size="$1";
  local -i flag=1;
  for ((r=1;r<size;++r)){
    for ((i=0;i<r;++i)){
      #echo `$(($1-$2)) | sed -e "s/^-//g"`;
      if (( board[i]>=board[r] ));then
        val=$(( board[i]-board[r] ));
      else
        val=$(( board[r]-board[i] ));
      fi

      if (( board[i]==board[r] || val==(r-i) ));then
        flag=0; 
      fi
    }
  }
  [[ $flag -eq 0 ]]
  return $?;
}
#
: '非再帰版ブルートフォース';
function bluteForce_NR()
{
  local -i size="$1";
  local -i row="$2";
  for ((i=0;i<size;i++)){ board[$i]=-1; }
  while ((row>-1));do
    local -i matched=0;
    local -i col=0;  
    for((col=board[row]+1;col<size;col++)){
      board[$row]=$col;
      matched=1;
      break;
    }
    if ((matched));then
      ((row++));
      if ((row==size));then  # 最下部まで到達
        ((row--));
        check_bluteForce "$size";  # 効きをチェック
        if (($?==1));then # 直前のreturnを利用
          ((TOTAL++));
          if (( DISPLAY==1 ));then
            printRecord "$size";# 出力
          fi
        fi
      fi
    else
      if ((board[row]!=-1));then
        board[$row]=-1;
      fi
      ((row--));
    fi
 done  
}
#
: '再帰版ブルートフォース';
function bluteForce_R()
{
  local -i size="$1";
  local -i row="$2";
  local -i col=;
  if ((row==size));then
    check_bluteForce "$size";
    if (( $?==1 ));then 
      ((TOTAL++));
      if (( DISPLAY==1 ));then
        printRecord "$size";# 出力
      fi
    fi
  else
    #for(( col=0;col<(size-row);col++ )){
    for(( col=0;col<size;col++ )){
      board["$row"]="$col";
      bluteForce_R  $size $((row+1));
    }
  fi
}
#
function NQ()
{
  local selectName="$1";
  local -i max=15;
  local -i min=4;
  local -i N="$min";
  local -i mask=0;
  local -i bit=0
  local -i row=0;
  local startTime=0;
	local endTime=0;
	local hh=mm=ss=0; 
  echo " N:        Total       Unique        hh:mm:ss" ;
  local -i N;
  for((N=min;N<=max;N++)){
    TOTAL=0; UNIQUE=0; COUNT2=0; row=0;
    mask=$(( (1<<N)-1 ));
    startTime=$(date +%s);# 計測開始時間

    "$selectName" "$N" "$row" "$mask" 0 0 0;

    endTime=$(date +%s); 	# 計測終了時間
    ss=$((endTime-startTime));# hh:mm:ss 形式に変換
    hh=$((ss/3600));
    ss=$((ss%3600));
    mm=$((ss/60));
    ss=$((ss%60));
    printf "%2d:%13d%13d%10d:%.2d:%.2d\n" $N $TOTAL $UNIQUE $hh $mm $ss ;
  } 
}

while :
do
read -n1 -p "
エイト・クイーン メニュー
実行したい番号を選択
5) ミラー
4) ビットマップ
3) 配置フラグ 
2) バックトラック 
1) ブルートフォース 

echo "行頭の番号を入力してください";

" selectNo;
echo 
case "$selectNo" in
  5)
    while :
    do 
      read -n1 -p "
      y|Y) ボード画面表示をする
      n|N) ボード画面表示をしない
      " select;
      echo; 
      case "$select" in
        y|Y) DISPLAY=1; break; ;;
        n|N) DISPLAY=0; break; ;;
      esac
    done
    while :
    do 
      read -n1 -p "
      y|Y) 再帰
      n|N) 非再帰
      " select;
      echo; 
      case "$select" in
        y|Y) NQ mirror_R; break; ;;
        n|N) NQ mirror_NR; break; ;;
      esac
    done
    ;;
  4)
    while :
    do 
      read -n1 -p "
      y|Y) ボード画面表示をする
      n|N) ボード画面表示をしない
      " select;
      echo; 
      case "$select" in
        y|Y) DISPLAY=1; break; ;;
        n|N) DISPLAY=0; break; ;;
      esac
    done
    while :
    do 
      read -n1 -p "
      y|Y) 再帰
      n|N) 非再帰
      " select;
      echo; 
      case "$select" in
        y|Y) NQ bitmap_R; break; ;;
        n|N) NQ bitmap_NR; break; ;;
      esac
    done
    ;;
  3)
    while :
    do 
      read -n1 -p "
      y|Y) ボード画面表示をする
      n|N) ボード画面表示をしない
      " select;
      echo; 
      case "$select" in
        y|Y) DISPLAY=1; break; ;;
        n|N) DISPLAY=0; break; ;;
      esac
    done
    while :
    do 
      read -n1 -p "
      y|Y) 再帰
      n|N) 非再帰
      " select;
      echo; 
      case "$select" in
        y|Y) NQ postFlag_R; break; ;;
        n|N) NQ postFlag_NR; break; ;;
      esac
    done
    ;;
  2)
    while :
    do 
      read -n1 -p "
      y|Y) ボード画面表示をする
      n|N) ボード画面表示をしない

      " select;
      echo; 
      case "$select" in
        y|Y) DISPLAY=1; break; ;;
        n|N) DISPLAY=0; break; ;;
      esac
    done
    while :
    do 
      read -n1 -p "
      y|Y) 再帰
      n|N) 非再帰

      " select;
      echo; 
      case "$select" in
    
        y|Y) NQ backTracking_R; break; ;;
        n|N) NQ backTracking_NR; break; ;;
      esac
    done
    ;;
  1)
    while :
    do 
      read -n1 -p "
      y|Y) ボード画面表示をする
      n|N) ボード画面表示をしない

      " select;
      echo; 
      case "$select" in
        y|Y) DISPLAY=1; break; ;;
        n|N) DISPLAY=0; break; ;;
      esac
    done
    while :
    do 
      read -n1 -p "
      y|Y) 再帰
      n|N) 非再帰

      " select;
      echo; 
      case "$select" in
        y|Y) NQ bluteForce_R; break; ;;
        n|N) NQ bluteForce_NR;break; ;;
      esac
    done
    ;;
  *)
    ;; 
esac
done
exit;

参考リンク

以下の詳細説明を参考にしてください。
【参考リンク】Ｎクイーン問題過去記事一覧
 【Github】エイト・クイーンのソース置き場 BashもJavaもPythonも！

Ｎクイーン問題（５０）第七章マルチプロセス Python編
https://suzukiiichiro.github.io/posts/2023-06-21-04-n-queens-suzuki/
Ｎクイーン問題（４９）第七章マルチスレッド Python編
https://suzukiiichiro.github.io/posts/2023-06-21-03-n-queens-suzuki/
Ｎクイーン問題（４８）第七章シングルスレッド Python編
https://suzukiiichiro.github.io/posts/2023-06-21-02-n-queens-suzuki/
Ｎクイーン問題（４７）第七章クラス Python編
https://suzukiiichiro.github.io/posts/2023-06-21-01-n-queens-suzuki/
Ｎクイーン問題（４６）第七章ステップＮの実装 Python編
https://suzukiiichiro.github.io/posts/2023-06-16-02-n-queens-suzuki/
Ｎクイーン問題（４５）第七章キャリーチェーン Python編
https://suzukiiichiro.github.io/posts/2023-06-16-01-n-queens-suzuki/
Ｎクイーン問題（４４）第七章　対象解除法 Python編
https://suzukiiichiro.github.io/posts/2023-06-14-02-n-queens-suzuki/
Ｎクイーン問題（４３）第七章　ミラー Python編
https://suzukiiichiro.github.io/posts/2023-06-14-01-n-queens-suzuki/
Ｎクイーン問題（４２）第七章　ビットマップ Python編
https://suzukiiichiro.github.io/posts/2023-06-13-05-n-queens-suzuki/
Ｎクイーン問題（４１）第七章　配置フラグ Python編
https://suzukiiichiro.github.io/posts/2023-06-13-04-n-queens-suzuki/
Ｎクイーン問題（４０）第七章　バックトラック Python編
https://suzukiiichiro.github.io/posts/2023-06-13-03-n-queens-suzuki/
Ｎクイーン問題（３９）第七章　バックトラック準備編 Python編
https://suzukiiichiro.github.io/posts/2023-06-13-02-n-queens-suzuki/
Ｎクイーン問題（３８）第七章　ブルートフォース Python編
https://suzukiiichiro.github.io/posts/2023-06-13-01-n-queens-suzuki/
Ｎクイーン問題（３７）第六章 C言語移植その１７ pthread並列処理完成
https://suzukiiichiro.github.io/posts/2023-05-30-17-n-queens-suzuki/
Ｎクイーン問題（３６）第六章 C言語移植その１６ pthreadの実装
https://suzukiiichiro.github.io/posts/2023-05-30-16-n-queens-suzuki/
Ｎクイーン問題（３５）第六章 C言語移植その１５ pthread実装直前版完成
https://suzukiiichiro.github.io/posts/2023-05-30-15-n-queens-suzuki/
Ｎクイーン問題（３４）第六章 C言語移植その１４
https://suzukiiichiro.github.io/posts/2023-05-30-14-n-queens-suzuki/
Ｎクイーン問題（３３）第六章 C言語移植その１３
https://suzukiiichiro.github.io/posts/2023-05-30-13-n-queens-suzuki/
Ｎクイーン問題（３２）第六章 C言語移植その１２
https://suzukiiichiro.github.io/posts/2023-05-30-12-n-queens-suzuki/
Ｎクイーン問題（３１）第六章 C言語移植その１１
https://suzukiiichiro.github.io/posts/2023-05-30-11-n-queens-suzuki/
Ｎクイーン問題（３０）第六章 C言語移植その１０
https://suzukiiichiro.github.io/posts/2023-05-30-10-n-queens-suzuki/
Ｎクイーン問題（２９）第六章 C言語移植その９
https://suzukiiichiro.github.io/posts/2023-05-30-09-n-queens-suzuki/
Ｎクイーン問題（２８）第六章 C言語移植その８
https://suzukiiichiro.github.io/posts/2023-05-30-08-n-queens-suzuki/
Ｎクイーン問題（２７）第六章 C言語移植その７
https://suzukiiichiro.github.io/posts/2023-05-30-07-n-queens-suzuki/
Ｎクイーン問題（２６）第六章 C言語移植その６
https://suzukiiichiro.github.io/posts/2023-05-30-06-n-queens-suzuki/
Ｎクイーン問題（２５）第六章 C言語移植その５
https://suzukiiichiro.github.io/posts/2023-05-30-05-n-queens-suzuki/
Ｎクイーン問題（２４）第六章 C言語移植その４
https://suzukiiichiro.github.io/posts/2023-05-30-04-n-queens-suzuki/
Ｎクイーン問題（２３）第六章 C言語移植その３
https://suzukiiichiro.github.io/posts/2023-05-30-03-n-queens-suzuki/
Ｎクイーン問題（２２）第六章 C言語移植その２
https://suzukiiichiro.github.io/posts/2023-05-30-02-n-queens-suzuki/
Ｎクイーン問題（２１）第六章 C言語移植その１
N-Queens問://suzukiiichiro.github.io/posts/2023-05-30-01-n-queens-suzuki/
Ｎクイーン問題（２０）第五章並列処理
https://suzukiiichiro.github.io/posts/2023-05-23-02-n-queens-suzuki/
Ｎクイーン問題（１９）第五章キャリーチェーン
https://suzukiiichiro.github.io/posts/2023-05-23-01-n-queens-suzuki/
Ｎクイーン問題（１８）第四章エイト・クイーンノスタルジー
https://suzukiiichiro.github.io/posts/2023-04-25-01-n-queens-suzuki/
Ｎクイーン問題（１７）第四章　偉人のソースを読む「Ｎ２４を発見ＪｅｆｆＳｏｍｅｒｓ」
https://suzukiiichiro.github.io/posts/2023-04-21-01-n-queens-suzuki/
Ｎクイーン問題（１６）第三章　対象解除法ソース解説
https://suzukiiichiro.github.io/posts/2023-04-18-01-n-queens-suzuki/
Ｎクイーン問題（１５）第三章　対象解除法ロジック解説
https://suzukiiichiro.github.io/posts/2023-04-13-02-nqueens-suzuki/
Ｎクイーン問題（１４）第三章　ミラー
https://suzukiiichiro.github.io/posts/2023-04-13-01-nqueens-suzuki/
Ｎクイーン問題（１３）第三章　ビットマップ
https://suzukiiichiro.github.io/posts/2023-04-05-01-nqueens-suzuki/
Ｎクイーン問題（１２）第二章　まとめ
https://suzukiiichiro.github.io/posts/2023-03-17-02-n-queens-suzuki/
Ｎクイーン問題（１１）第二章　配置フラグの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-17-01-n-queens-suzuki/
Ｎクイーン問題（１０）第二章　バックトラックの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-16-01-n-queens-suzuki/
Ｎクイーン問題（９）第二章　ブルートフォースの再帰・非再帰
https://suzukiiichiro.github.io/posts/2023-03-14-01-n-queens-suzuki/
Ｎクイーン問題（８）第一章　まとめ
https://suzukiiichiro.github.io/posts/2023-03-09-01-n-queens-suzuki/
Ｎクイーン問題（７）第一章　ブルートフォース再び
https://suzukiiichiro.github.io/posts/2023-03-08-01-n-queens-suzuki/
Ｎクイーン問題（６）第一章　配置フラグ
https://suzukiiichiro.github.io/posts/2023-03-07-01-n-queens-suzuki/
Ｎクイーン問題（５）第一章　進捗表示テーブルの作成
https://suzukiiichiro.github.io/posts/2023-03-06-01-n-queens-suzuki/
Ｎクイーン問題（４）第一章　バックトラック
https://suzukiiichiro.github.io/posts/2023-02-21-01-n-queens-suzuki/
Ｎクイーン問題（３）第一章　バックトラック準備編
https://suzukiiichiro.github.io/posts/2023-02-14-03-n-queens-suzuki/
Ｎクイーン問題（２）第一章　ブルートフォース
https://suzukiiichiro.github.io/posts/2023-02-14-02-n-queens-suzuki/
Ｎクイーン問題（１）第一章　エイトクイーンについて
https://suzukiiichiro.github.io/posts/2023-02-14-01-n-queens-suzuki/

最新技術やプログラム、デザインなど様々な情報を提供するサイト

Ｎクイーン問題（１４）第三章　ミラー

ミラー

奇数と偶数

図解すると

奇数・偶数共通通過ブロック解説

奇数ブロック解説

ロジック部分解説

ミラー版ソースコード

まとめ版のソースコード

参考リンク

書籍の紹介

suzukiiichiro

サイト内検索

Ｎクイーン問題（１４）第三章 ミラー

ミラー

奇数と偶数

図解すると

奇数・偶数共通通過ブロック解説

奇数ブロック解説

ロジック部分解説

ミラー版ソースコード

まとめ版のソースコード

参考リンク

書籍の紹介

Ｎクイーン問題（１５）第三章 対象解除法 ロジック解説

Ｎクイーン問題（１３）第三章 ビットマップ

suzukiiichiro

サイト内検索

Ｎクイーン問題（１４）第三章　ミラー

Ｎクイーン問題（１５）第三章　対象解除法ロジック解説

Ｎクイーン問題（１３）第三章　ビットマップ